[통계] 정규화(Normalization) vs 표준화(Standardization)

 

ML을 공부하는 사람이라면 feature scaling이 얼마나 중요한 지 알것이다. scikit-learn에는 많은 스케일링 메서드들이 모듈화 되어있는데, 기본적으로 정규화와 표준화가 무엇인지 이해해야 과제를 수행하기 적합한 방법을 선택할 수 있다.

 

이 포스트를 기반으로 작성하였다.

 

 

정규화 (Normalization)

  정규화의 목적은 데이터셋의 numerical value 범위의 차이를 왜곡하지 않고 공통 척도로 변경하는 것이다. 기계학습에서 모든 데이터셋이 정규화 될 필요는 없고, 피처의 범위가 다른 경우에만 필요하다.

  위의 표에서의 데이터를 가정해보자. 데이터셋은 나이\( (X_1) \)과 월별 소득\( (X_2) \)의 두 개의 피처로 이루어져 있다. 모든 관측개체를 살피지 않았으나 우리는 나이의 범위가 [0~100]이고 월별 소득은 [0~10,000,000] 혹은 그 이상으로 예상해볼 수 있다. 월별 소득은 나이의 약 100,000배이며 범위의 range도 훨씬 넓다. 따라서 이 두 가지 피처는 매우 다른 범위에 있다고 말할 수 있다. 이 데이터셋을 그냥 활용한다면, 예를 들어 다변량 선형회귀 분석과 같은 분석을 수행할 때, 소득은 본질적으로 더 큰 값으로 인해 결과에 더 큰 영향을 미친다. 그렇다고 해서 소득이 나이라는 피처보다 더 중요한가? 아닐 것이다.

Since both the features have different scales, there is a chance that higher weightage is given to features with higher magnitude. This will impact the performance of the machine learning algorithm and obviously, we do not want our algorithm to be biassed towards one feature.
Therefore, we scale our data before employing a distance based algorithm so that all the features contribute equally to the result.

 - 출처 : https://www.analyticsvidhya.com/blog/2020/04/feature-scaling-machine-learning-normalization-standardization/

 

  따라서 정규화를 통해 피처 벡터의 유클리디안 길이가 1이 되도록 데이터 포인트를 조정한다. 다른 말로 하면 지름이 1인 원(3차원이라면 구)에 데이터 포인트를 투영한다. 즉, 각 데이터 포인트가 다른 비율로 스케일이 조정된다는 것이다. 이러한 정규화는 특성 벡터의 길이는 상관 없고 데이터의 방향만이 중요할 때 많이 사용한다.

 

Min-Max Scaling

  Min-Max Scaling은 모든 피처가 정확하게 [0,1] 사이에 위치하도록 데이터를 변경한다. 2차원 데이터셋일 경우에는 모든 데이터가 x축의 0과 1, y축의 0과 1 사이의 사각 영역에 담기게 된다.

  Min-Max Scaling은 다음과 같은 공식으로 구할 수 있다.

$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$

즉, 데이터에서 최솟값을 빼고 전체 범위로 나누는 것이다.

  아직도 헷갈리는 부분이다... 그래서 정규화=Min-Max Scaling인가? 사실 많은 인터넷 자료에서 두 개를 같은 개념으로 두고 보지만, 필자가 내린 결론으로는 Min-Max Scaling은 정규화를 하는 하나의 방법에 속한다. 따라서 \( Normalization\supset MinMax Scaling \)이라는 표현이 더 맞을 것이다. 위에 유클리디안 거리로 계산하는 방법은 scikit-learn의 Normalizer로 구현 가능하다. 

 

 

표준화 (Standardization)

  표준화(또는 Z-score 정규화)의 결과는 다음과 같은 표준정규분포의 속성을 갖도록 피처가 재조정되는 것이다.

$$ \mu = 0, \sigma = 1 $$

여기서 \( \mu \)는 평균이고 \( \sigma \)는 평균으로부터의 표준편차이다. 표본의 표준 점수(Z-score)는 다음과 같이 계산된다.

$$ z = \frac{x - \mu}{\sigma} $$

 

  0 주위에 표준편차 1의 값으로 배치되도록 피처를 표준화하는 것은 다른 단위를 가진 측정값을 비교할 때 중요할 뿐만 아니라 많은 기계 학습 알고리즘의 일반적인 요구 사항이다. 직관적으로, 우리는 경사하강법을 두드러진 예로 생각할 수 있다(로지스틱 회귀분석, SVM, 퍼셉트론, 신경망 등에 자주 사용되는 최적화된 알고리즘). 피처들이 각각 다른 척도에 있으면, 피처값 \( x_j \)가 \( w_j := w_j + \Delta w_j \)가 업데이트 되도록 가중치 업데이트의 역할을 하기 때문에 특정 가중치가 다른 가중치보다 더 빨리 업데이트 될 수 있다. 반대로 말하면, 피처값의 범위가 비슷하면 경사하강법은 더 빠르게 최저값으로 수렴하게 된다. 

$$ \Delta w_j = -\eta \frac{\partial J}{\partial w_j} = \eta \sum_i (t^{(i)} - o^{(i)})x_j^{(i)} $$

• \( \eta \)는 learning rate, \( t \)는 타겟 클래스의 레이블, \( o \)는 실제 output

  이해하면 알겠지만 위 설명은 feature scaling이라는 큰 개념에 해당되는 것이다. 즉, 정규화와 표준화 모두 경사 하강 알고리즘을 더 빠르게 동작할 수 있도록 도와주는 것이다. 신경망에서의 gradient descent에 대해 시각화를 통해서 더 자세하게 알고 싶으면 Hinton 교수님의 Coursera 강의를 추천한다. 

  표준화 방법은 특성의 최솟값과 최댓값 크기를 제한하지는 않는다. 즉, 이상치(outlier)를 파악할 수 있는데, Z-score을 구함으로써 데이터가 평균으로부터 얼마나 떨어져있는지 구한 다음, 특정 범위를 벗어난 데이터는 이상치로 간주해 제거할 수 있다. 필자의 이 포스트에서 표준정규분포곡선을 다루면서 '68-95-99.7법칙'을 언급한 적이 있다. 이에 따르면 표준화한 Z값이 간단히는 \( \pm 2\sigma \) 안에 있으면 95% 신뢰구간 내에 있는 것이므로, 이 데이터만 선택하게 되면 이상치를 제거할 수 있다.

정규화된 데이터와 표준화된 데이터의 분포의 차이를 단적으로 보여준다.

 

 

 

Normalization vs Standardization

  두 feature scaling 방식의 차이점을 정리해보았다.

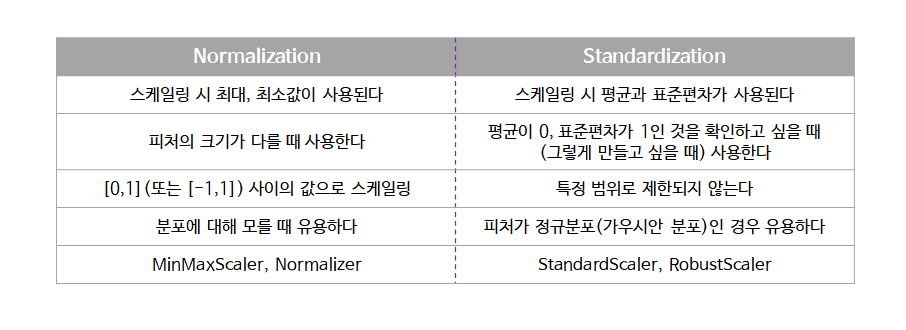
  그렇다면 언제 정규화를 하고 언제 표준화를 할까? 명확한 답은 없다. 통상적으로는 표준화를 통해 이상치를 제거하고, 그 다음 데이터를 정규화 해 상대적 크기에 대한 영향력을 줄인 다음 분석을 시작한다고 한다.

예를 들어, cluster analysis에서 특정 거리 측도를 기반으로 피처 간의 유사성을 비교하기 위해 표준화가 특히 중요할 수도 있다. 또 다른 예는 주성분 분석(Principal Component Analysis)로, 보통 Min-Max Scaling보다 표준화를 선호한다. 왜냐하면 분산을 극대화하는 성분에 관심이 있기 때문이다. 정규화는 이미지 프로세싱에서 자주 사용되는데, pixel intensities를 특정 범위(RGB 색상 범위의 경우 0~255) 내에 맞추려면 정규화가 필요하다. 

 

In addition, we’d also want to think about whether we want to “standardize” or “normalize” (here: scaling to [0, 1] range) our data. Some algorithms assume that our data is centered at 0. For example, if we initialize the weights of a small multi-layer perceptron with tanh activation units to 0 or small random values centered around zero, we want to update the model weights “equally.” As a rule of thumb I’d say: When in doubt, just standardize the data, it shouldn’t hurt. (대충 데이터를 표준화해서 나쁠 거 없다는 뜻)

 - 출처 : https://sebastianraschka.com/Articles/2014_about_feature_scaling.html#about-standardization