[통계] 여러가지 분포 - 정규분포, 이항분포, t-분포, 카이제곱-분포

 

이 포스트에서는 추후 헷갈리지 않도록 각 분포별 정의와 수식, 특징을 정리해보려고 한다.

 

1. 정규분포 (normal distribution)

 관측된 자료를 이용하여 그린 히스토그램을 경험적 히스토그램(empirical histogram)이라고 부른다. 사실상 대부분의 히스토그램은 단위변환이나 표준화되지 않은 경험적 히스토그램이다. 그렇다면 경험적 히스토그램을 평가하거나 근사시킬 하나의 기준이 있을까? 그 기준 중 하나가 정규분포곡선이다.

 - 출처: 통계학, 제3판 (류근관 저)

 

  벨기에 수학자 아돌프 케틀레(Adolphe Quetelet, 1796-1874)는 정규분포곡선을 하나의 이상적인 히스토그램으로 생각했고, 실제 자료를 통해 얻어낸 히스토그램을 비교할 하나의 기준으로 정규분포곡선을 이용하였다. 이는 중심극한정리에 의하여 독립적인 확률변수들의 평균은 정규분포에 가까워지는 성질이 있기 때문이다. 중심극한정리(central limit function)는 동일한 확률분포를 가진 독립확률변수 n개의 평균의 분포는 n이 적당히 크다면 정규분포에 가까워진다는 정리이다.

  평균이 \( \mu \)이고 표준편차가 \( \sigma \)인 정규분포곡선의 식은 다음과 같이 표현된다.

$$ f(x) = \frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{1}{2} \left ( \frac{x-\mu}{\sigma} \right )^2}, -\infty < x < +\infty $$

 

\( f(x) \)는 확률밀도함수(probability density function)이다. 이는 밀도단위(density scale)을 써서 확률과 관련된 개념을 나타내주는 함수이다.

  정규분포곡선은 실제자료의 분포가 아니라 실제자료의 분포를 근사시켜 줄 하나의 수학적 모형이다. 이는 개념상 모집단에 해당한다. 그래서 평균과 표준편차를 표기할 때 영어 알파벳 대신 그 모태가 되는 그리스 문자 \( \mu \)와 \( \sigma \)를 사용했다. 이러한 인식을 기반으로 우리는 \( \mu \)를 모평균, \( \sigma \)를 모표준편차라고 부르기로 했다.

 

 

정규분포곡선은 \( \mu \)와 \( \sigma \) 값에 따라 중심과 퍼진 정도는 달라지나 전반적인 모양은 변하지 않는다

정규분포곡선의 성질:

• 평균을 중심으로 좌우 대칭이다(symmetric)
• 종 모양을 띈다(bell-shaped)
• 봉우리가 하나이다(single-peaked)

  평균이 0, 표준편차가 1인 정규분포를 특별히 표준정규분포(standard normal distribution)라고 한다. 확률변수 \( Z \)가 표준정규분포를 따를 때, 이를 \( Z \sim N(0,1) \)로 표시한다. 표준정규분포의 확률밀도함수는 다음과 같다.

$$ f(z) = \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2} z^2}, -\infty < z < +\infty $$

 

  표준정규분포와 관련해 다음의 68-95-99.7 법칙이 있다.

 

 

 

 

2. 이항분포 (binomial distribution)

  남과 여, 합격과 불합격 등 결과가 둘로 나뉘는 시행을 베르누이 시행이라고 하고, 베르누이 시행에서 성공에 1을, 실패에 0을 대응시키는 확률변수를 베르누이 확률변수(Bernoulli random variable)이라고 한다.

  성공확률이 p로 동일한 베르누이 시행을 독립적으로 n번 반복한다고 하자. 총 횟수를 \( X \)라 하면, \( X = X_1 + X_2 + ... + X_n \)로 표시할 수 있다. 이때 \( X \)는 이항분포를 따르는 이항확률변수라 한다. 이항분포는 시행횟수 n이 고정되어 있고 각각의 베르누이 시행이 독립적이며, 동일한 성공확률 p를 공유할 때만 사용된다. 기호로는 \( X \sim B(n,p) \)로 나타낸다.

 

 

  이항분포에서 확률은 이항공식을 써서 구한다. n번의 시행 중 k번 성공할 확률은 다음의 이항공식에 의해 구할 수 있다.

$$ p(X=k) = \frac{n!}{k!(n-k)!} p^k(1-p)^(n-k), k=0,1,...,n $$

 

• n은 시행횟수, k는 성공횟수, p는 성공확률을 나타낸다.
• 이항공식은 이항분포와 마찬가지로, n의 값은 미리 정해져 있고 매번의 시행은 상호독립이며 p는 매 시행마다 동일하다는 조건하에서 성립한다.

이항공식의 첫 번째 부분인 \( \frac{n!}{k!(n-k)!} \)은 이항계수로, 'n개 중 k개를 뽑아 만들 수 있는 조합의 수'를 나타내기 때문에 \( \binom{n}{k} \) 또는 \( _{n}\textrm{C}_{k} \)로 표기한다.

 

 

 

3. t-분포

  표본의 크기가 크지 않고 질적인 자료도 아니면 t-검정(t-test)를 주로 사용한다. 신뢰도를 높이기 위해 표본을 많이 구하면 되지만 현실에서는 시간과 비용의 제약으로 표본을 많이 확보하지 못하는 경우도 있어, 이런 경우에는 정규분포보다 한 단계 예측범위가 넓은 t-분포를 이용하는 것이다. 

 

 

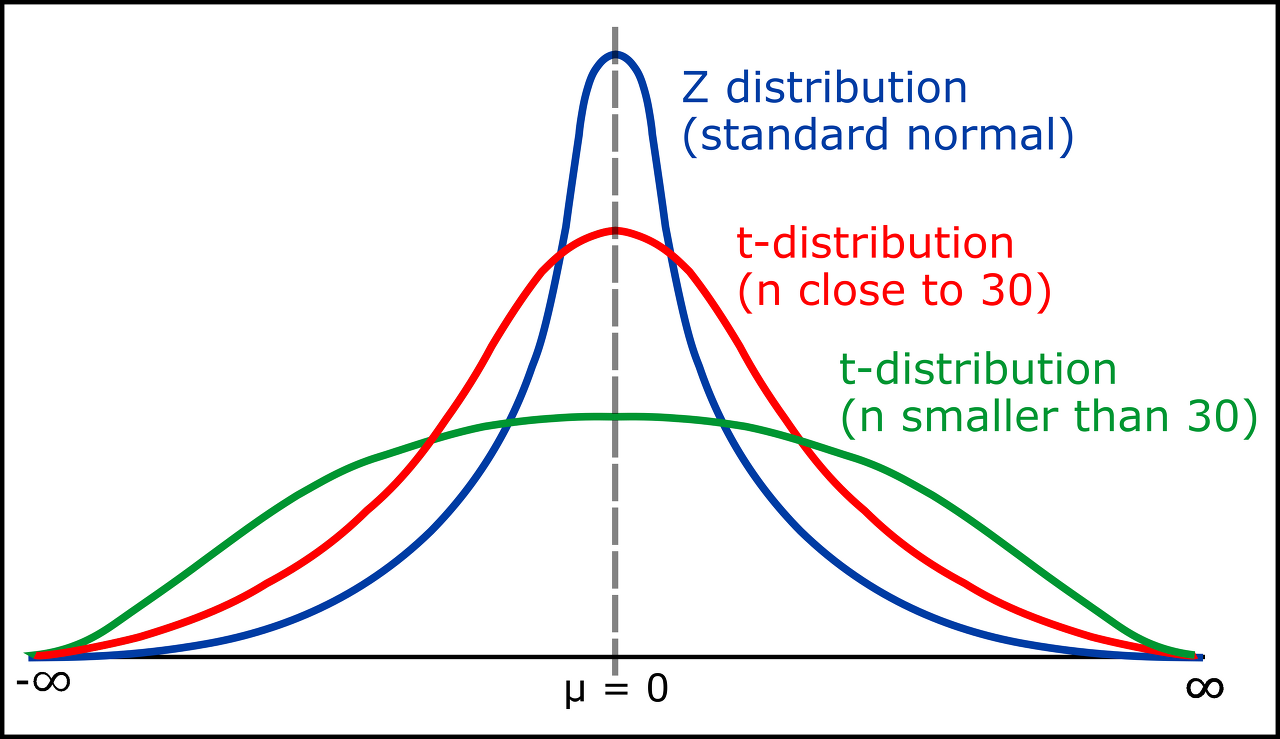
  그림에서 볼 수 있다싶이 표본의 수가 많아질수록 t-분포의 그래프는 점점 표준정규분포와 비슷해지고, 표본의 수가 적어질수록 그래프는 옆으로 퍼지는 형태가 된다(표본의 수가 적을수록 실험의 신뢰도는 낮아지기 때문에, 예측범위를 넓히기 위해서 그래퍼가 퍼지는 것이라고 한다). t-분포는 자유도 \( v = n-1 \)에 따라 모양이 결정된다.

 

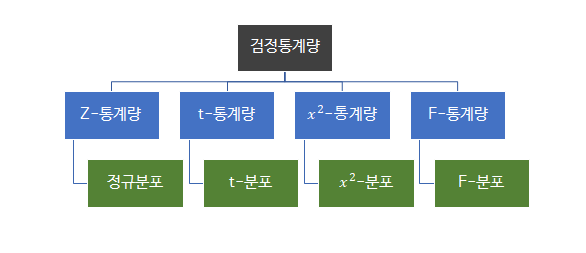
  우리는 어떤 가설에 대해 유의성을 검정할 때 귀무가설과 대립가설을 세운다. 그 후 잠정적으로 일단 귀무가설이 맞다고 가정한다. 이런 전제 하에 검정통계량을 계산해 유의수준을 구한 다음 귀무가설을 기각시킬지 말지를 결정한다. 이때 구하는 이 검정통계량은 확률분포에 따라 계산식이 달라지는데, 정규분포와 카이제곱분포, t분포, F분포 등을 활용한다.

t-분포에서는 Z-분포와는 달리 모집단의 표준편차를 모른다고 가정하기 때문에 표본 표준편차를 근거로 한다. 모평균 \( \mu \)의 점추정량은 표본평균 \( \overline{X} \)라 하고, 표본 표준편차를 \( s \)라고 하면

$$ t = \frac{\overline{X} - \mu}{s/\sqrt{n}} \sim t(n-1) $$

n는 관측치의 개수이다. 

 

모평균을 알고 있다면 

$$ \hat{\sigma^2} = \frac{\sum_{i=1}^n (x_i-\mu)^2}{n} $$

을 사용하면 좋겠지만, 우리는 대부분의 경우 모집단의 모평균과 모표준편차를 모르는 상태에서 표본을 추출해 검정을 하므로 관측치 \( x_1, x_2,..., x_n \) 중 어느 하나는 자유롭게 들어갈 수 없다. 따라서 자유도는 n-1과 표본평균 \( \overline{x} \)를 갖는 다음의 식을 사용한다.

$$ \hat{s^2} = \frac{\sum_{i=1}^n (x_i-\overline{x})^2}{n-1} $$

 

아니면 이렇게 생긴 t-분포표에서 자유도와 유의수준 \( \alpha \)를 통해 t-값을 구할 수 있다.

 

 

 

4. 카이제곱-분포 (chi-square distribution)

  \( x^2 \)-검정은 범주별로 관측된 빈도(observed frequency)와 기대빈도(expected frequency)의 차이를 봄으로써 주어진 자료가 특정한 확률모형으로부터 얻어졌는지 검정하는데 쓰인다. 칼 피어슨(Karl Pearson, 1857-1936)이 고안했다. \( x^2 \)-분포도 t-분포와 같은 맥락으로 검정을 위한 통계량을 구하는데 쓴다.

  그래서 카이제곱이란 무엇인가? 주사위를 던지는 예를 들어보자. 우리는 주사회 60회를 던지면, 1부터 6까지의 숫자가 각각 한 장씩 들어있는 상자로부터 60회 복원추출한 결과와 비슷할 것을 기대한다. 즉, 범주별로 기대도수가 10이다. 하지만 다음과 같은 실제 관측도수가 나왔다고 해보자.

위의 표에서 3과 4가 너무 많이 나왔다. 그러면 주사위에 문제가 있는 것인가? 섣불리 판단하지 말고 \( x^2 \)-통계량을 계산해보자. 표의 모든 행에서 관측된 도수는 기대도수와의 차이를 보인다. 이제 각각의 관측된 도수와 기대도수의 차이를 한꺼번에 모아서 차이의 척도를 구해보자. \( x^2 \)-통계량은 각 행별로 차이를 구하여 제곱하고 이를 기대도수로 나눈 뒤 합쳐서 구한다.

$$ x^2 = \sum \frac{(관측된 도수 - 기대도수)^2}{기대도수} $$

이를 수식화하면 다음과 같다.

$$ x^2 = \sum_{i=1}^n \frac{(O_i - E_i)^2}{E_i} $$

 

  표준정규분포를 따르고 서로 독립인 n개의 확률변수 \( Z_1, Z_2, ..., Z_n \)을 각각 제곱하여 합치면 그 합은 자유도가 n인 \( x^2 \)-분포를 따른다.

$$ x^2 = Z_1^2 + Z_2^2 + ... + Z_n^2 \sim x^2(n) $$

 

\( Z_1, Z_2, ..., Z_n \)이 n개의 상호독립인 확률변수로서 각각 평균이 0이고 분산이 1인 표준정규분포를 따른다고 할 때, 이 Z들을 제곱하여 합한 값으로 정의되는 새로운 확률변수 X는 자유도가 \( x^2 \)-분포를 따른다. 이를 \( X = \sum (Z_i^2) - X^2(n) \)이라고 표현한다. 즉, \( X \sim N(\mu, \sigma) \)일 때, \( Z = \frac{(X-\mu)}{\sigma} \)를 따르고, 이 표준정규변수 Z를 제곱한 \( Z^2 = \frac{(X-\mu)^2}{\sigma^2} \)는 자유도가 1인 \( X^2(1) \)을 따르게 된다. 즉, \( Z^2 \sim X^2(1) \)이다.

 

 

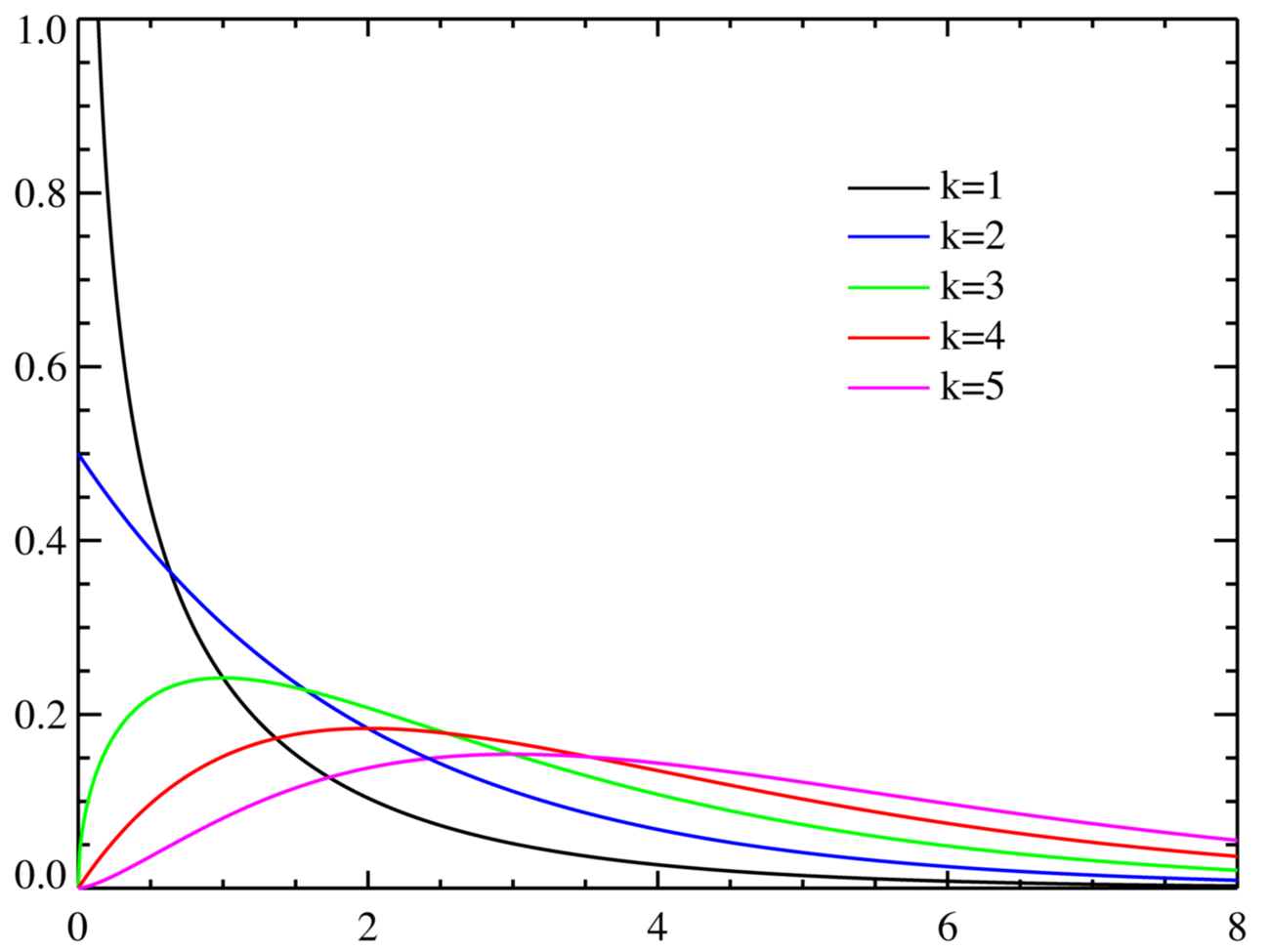
지금까지 봐왔던 확률분포들과 다르게 \( x^2 \)-분포는 종형이 아니다. 단, n의 크기(사진에서는 k의 크기가 되겠다)가 증가하게 되면 점점 대칭성을 갖추게 된다. 또, \( x^2 \)-value는 제곱값이므로 0보다 항상 크다.

 

\( x^2 \)-분포도 자유도에 따라 달라지기 때문에 분포표가 있다.

 

 

 

나머지 분포들은 다음 시간에.....