우리는 이 포스트에서 로지스틱 회귀에 대해 살펴보았다. 로지스틱 회귀를 어떻게 적합시킬까? 다른 회귀 모형이 그러하듯 로지스틱 회귀도 모형의 모수를 추정함으로써 적합시킨다. 로지스틱 회귀에서 적합은 로짓을 가지고 이루어진다. 로짓 변환(logit transformation)은 모수에 선형인 모형을 생성하는데, 이를 이용한 추정에 사용되는 방법이 최대우도법이다. 최대우도법은 로지스틱 회귀의 모수를 추정하는 것뿐만 아니라 각종 분포의 모수를 구하는데 고루 쓰인다.
우도(likelihood)란 어떤 일이 발생할 가능성을 말한다. 최대우도법(maximum likelihood estimation; MLE)이란 어떤 확률변수에서 표집한 값들을 토대로 각 가설마다 계산된 우도값 중 가장 큰 값을 고르는 통계적 추정방법이다. 쉽게 말하면 우리가 알고 싶은 데이터 \( \Theta \)(모수)가 있다고 할 때, 여러 관측치들을 통해서 그러한 관측치가 나오게 하는 가장 그럴 듯한 값(가능성이 높은 값)을 추정하는 것이다.
이 영상을 보고 정리했음을 미리 알린다.
1. 기본 가정
\( \Theta \)를 알지 못하는 미지의 값(모수)라고 할 때,
- 어떤 모수 \( \Theta \)fh 결정되는 확률변수들의 모임 \( X_1, X_2, ..., X_n \)이 있다고 할 때, 이에 대한 확률질량함수, 혹은 확률밀도함수를 \( f(X|\Theta) \)라 한다. 이때 확률변수들에서 무작위 추출(random sampling)을 통해 뽑은 각각의 표본을 \( x_1, x_2, ..., x_n \)이라 한다.
- 확률변수 \( X_1, X_2, ..., X_n \)은 서로 독립이고 동일한(independently and identically distributed; iid) 분포를 가진다.
2. 우도함수 (likelihood function)
최대우도함수를 살펴보기 전에 우도함수를 먼저 알아보자. 우도함수는 표본 \( x_1, x_2, ..., x_n \)의 결합확률밀도함수 f를 모수 \( \Theta \)에 대한 함수로 볼 때를 말하며
$$ L(\Theta|x_1,...,x_n) $$
으로 표기한다.
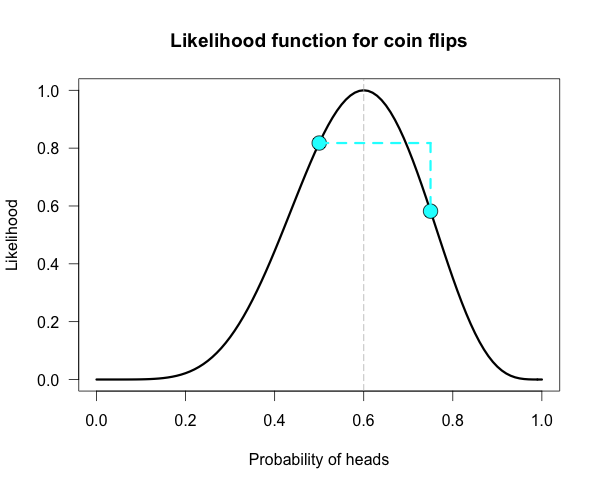
예를 들어, 동전 10개를 던졌을 때 앞면이 나올 확률에 대한 우도함수가 있다고 하자. x축은 \( \Theta \), y축은 \( L(\Theta) \)이다. 왼쪽에 찍힌 점의 x값을 \( \Theta_1 \), 오른쪽에 찍힌 점의 x값을 \( \Theta_2 \)라고 했을 때, 당연하게도 \( L(\Theta_1) \)이 \( L(\Theta_2) \)보다 크다. 즉 동전을 던졌을 때 \( \Theta_1 \)의 확률로 앞면이 나올 가능성이 \( \Theta_2 \)의 확률로 앞면이 나올 가능성보다 크다는 뜻이다.
우도함수는 표본 \( x_1, ..., x_n \)의 결합확률밀도함수(joint probability density function)이다. 이를 f라고 하면, 확률변수들은 서로 독립이기 때문에
$$ f( x_1,...,x_n|\Theta) = f(x_1|\Theta) ... f(x_n|\Theta) $$
즉,
$$ L(\Theta|x_1,...,x_n) = \coprod_{i=1}^n f(x_i|\Theta) $$
3. 최대우도추정치 (maximum likelihood estimator)
최대우도추정치는 우도함수를 최대화하는 \( \Theta \)를 말한다. 일반적으로 우도함수가 최대가 되는 모수 \( \Theta \)를 추정치로 채택하는 방법으로는 우도함수를 최대화시킬 수 있도록 \( \Theta \)에 대해 미분하는 방법을 사용한다.
$$ \frac{\partial}{\partial\Theta}L(\Theta|x) = 0 $$
우도함수를 최대로 만드는 \( \hat{\Theta} \)를 다음과 같이 쓰기도 한다.
$$ \hat{\Theta} = argmax_0L(\Theta) $$
4. 로그 우도함수 (log-likelihood function)
로그 우도함수, 혹은 로그 가능도는 우도함수의 로그이며, 확률변수가 독립확률변수로 나누어지는 경우와 같이 확률분포함수가 곱셈 꼴로 나올 때 미분 계산의 편의성을 위해 사용한다. 로그 함수는 단조 증가, 즉 왼쪽에서 오른쪽으로 줄곧 상승하기 때문에 우도함수에서 극값을 가지는 위치와 로그 우도함수에서 극값을 기지는 위치는 같다.
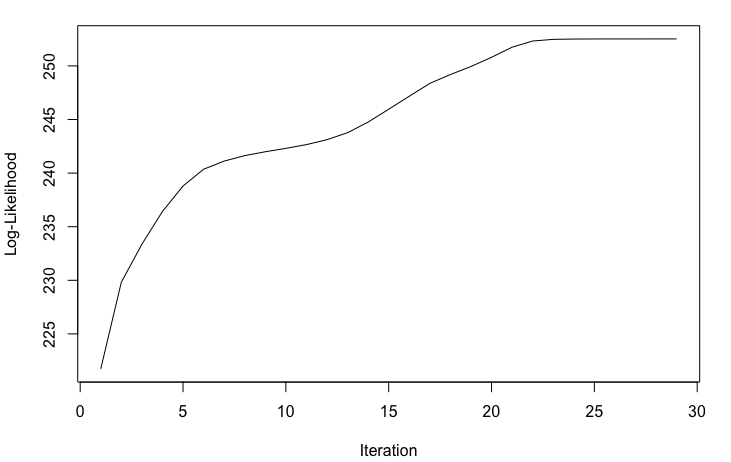
따라서 우도함수를 미분하여 극값을 구하는 대신, 로그 우도함수를 미분해도 같은 결과를 얻을 수 있다.
$$ L^*(\Theta) = log(L(\Theta)) = \sum_{i=1}^nlogf(x_i) $$
즉,
$$ \frac{\partial}{\partial\Theta} L^*(\Theta|x) = \frac{\partial}{\partial\Theta}logf(x_1,...,x_n|\theta ) = \sum_{i=1}^n\frac{\partial}{\partial\Theta}logf(x_i|\Theta) = 0 $$
Log-likelihood function is a logarithmic transformation of the likelihood function, often denoted by a lowercase l or \( \ell \) , to contrast with the uppercase L or \( \mathcal{L} \) for the likelihood. Because logarithms are strictly increasing functions, maximizing the likelihood is equivalent to maximizing the log-likelihood. But for practical purposes it is more convenient to work with the log-likelihood function in maximum likelihood estimation, in particular since most common probability distributions—notably the exponential family—are only logarithmically concave, and concavity of the objective function plays a key role in the maximization.
출처 - https://en.wikipedia.org/wiki/Likelihood_function#Log-likelihood
5. 최소제곱법과 최대우도법
우리는 단순선형회귀와 다중선형회귀에서 최소제곱법을 통해 모수를 추정했고, 로지스틱 회귀에서는 최대우도법을 통해 모수를 추정했다. 그렇다면 최소제곱법과 최대우도법의 차이는 무엇일까?
선형회귀에서는 말 그대로 y와 x가 선형 관계에 있다. 이때 모수를 추정하기 위해, 즉 회귀식을 적합시키기 위해 최소제곱법을 이용한다. 이전 포스트에서 설명한 것처럼 오차의 제곱의 합이 최소가 되는 해를 구하는 방법인데, 비교적 간단한 계산 방법이지만 데이터가 많아지면 계산량이 매우 증가한다는 단점이 있다고 한다.
y와 x가 선형 관계가 아닌 모형을 일반화선형모형(generalized linear model)이라 한다. 이때는 최대우도법을 이용한다. 통계적인 관점에서, 최대우도법는 대규모 데이터를 처리하는데 효과적이라고 한다. 뿐만 아니라 여러 가지 유형의 데이터에 다양하게 응용이 가능하고, 정밀한 추정치를 산출한다고 한다.
그리고 최대우도법은 오차항의 분포를 정규분포 \( N(0, \sigma^2) \)이라고 가정하여 얻은 것이고, 최소제곱추정치는 이러한 가정이 전제되어 있지 않다고 하는데... 사실 이해 못했다
참고 >> https://laoonlee.tistory.com/15
최우추정법 (MLE, Method of Maximum likelihood Estimation
저번에 최소제곱법으로 회귀계수 $\beta_0, \beta_1$을 추정했다면 (최소제곱법 내용은 여기!) 이번에는 최우추정법으로 추정하는 방법에 대해 알아보겠습니다! 최우추정법 MLE는 어떤 모수가 주어졌
laoonlee.tistory.com
'AI > Statistics' 카테고리의 다른 글
| [통계] F-분포와 분산 분석 ANOVA (0) | 2021.09.14 |
|---|---|
| [통계] 여러가지 분포 - 정규분포, 이항분포, t-분포, 카이제곱-분포 (0) | 2021.09.14 |
| [통계] logistic regression 예제 - 타이타닉 데이터셋 (0) | 2021.09.06 |
| [통계] 로지스틱 회귀와 정규화 (0) | 2021.09.06 |
| [통계] 다중회귀분석 예제 - Statsmodel을 이용한 고유값, vif 확인 (0) | 2021.09.06 |



