우리는 아래 포스트를 통해 최소제곱법과 회귀분석의 네 가지 기본 가정들을 살펴보았다. 이번 포스트에서는 회귀모형을 진단하는 방법들에 대해 알아보려 한다.
[통계] 최소제곱법과 회귀분석의 가정들, 회귀모형 진단
우리는 단순선형회귀와 다중선형회귀에서 최소제곱법을 통해 최소제곱추정치를 제시할 수 있다. 이 포스트에서는 최소제곱법이란 무엇인지 설명하고, 제시된 최소제곱추정량과 통계분석들이
heeya-stupidbutstudying.tistory.com
모형의 진단
회귀분석 결과의 진단(diagnosis)이란 회귀분석에 사용된 데이터가 회귀분석에 사용된 모형 가정을 제대로 만족하고 있는지를 확인하는 과정이다. 우리는 이를 위해 잔차를 사용한다.
종속변수 Y와 p개의 독립변수 \( X_1, X_2, ..., X_3 \)에 대한 n개의 관측개체들로 이루어져 있다고 할 때, 관측된 \( y \)값과 해당하는 적합값 \( \hat{y} \)식의 차이값은
$$ e_i = y_i - \hat{y_i} = y_i - \hat{\beta_0} - \hat{\beta_1}x_{i1} - \hat{\beta_2}x_{i2} - ... - \hat{\beta_p}x_{ip} $$
각 가정에 대한 진단 방법은 다음과 같다.
1. 선형성 검정
잔차 산점도(residual plot)
관측값 \( \hat{y} \)와 잔차 \( e \)의 산점도를 나타낸 것이다. 잔차 산점도를 통해 시각적으로 모형이 선형의 관계성을 나타내고 있는지 알 수 있다. (+등분산성 가정도)
- 정상적인 잔차 산점도
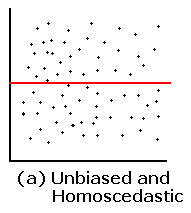
정상적인 잔차 산점도는 0을 중심으로 \( \hat{y} \)값에 관계없이 일정 범위 내에서 특정한 패턴을 가지지 않게 분포한다.
- 회귀모형의 비선형성(non-linearity) : 관측값 \( \hat{y} \)에 대하여 잔차 \( e \) 값이 곡선의 형태

두 이미지 모두 관측값이 증가함에 따라 y축 값인 잔차 \( e \)가 곡선의 형태를 띄는 것을 볼 수 있다. 우리는 최소제곱법을 통해 잔차의 제곱합을 최소화하는 하나의 선을 회귀식으로 추정한다. 하지만 다음과 같은 잔차 산점도가 발견된다면, 회귀식에 이차항을 포함시키라는 뜻으로 해석된다. 즉, 선형모형이 바람직하지 않다는 것으로 해석이 가능하다. 변수변환을 통해 독립변수의 모양을 변환시켜줌으로써 이를 해결할 수 있다.
- 회귀모형의 이분산성(heteroscedascity) : 관측값 \( \hat{y} \)가 증가함에 따라 잔차 \( e \) 값의 폭이 커지는 형태
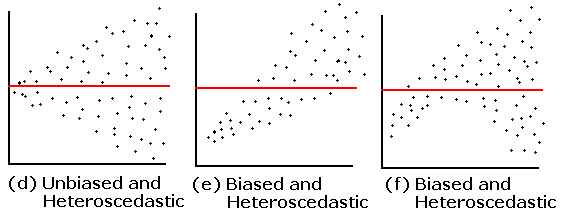
세 이미지 모두 관측값이 증가함에 따라 y축 값인 잔차 \( e \)값의 퍼짐 정도가 같이 증가하는 것을 볼 수 있다. 마찬가지로 변수변환을 통해 해결할 수 있는데, 종속변수 Y값을 그대로 사용하지 않고 변환하는 것이다.
$$ Y^*_i = log(Y_i) $$
$$ Y^*_i = \beta_0 + \beta_1x_i + \varepsilon_i, \varepsilon_i\sim iid N(0, \sigma^2) $$
이처럼 로그변환을 취하면 어느 정도 등분산성을 만족하게 된다.
2. 등분산성 검정
위에서처럼 그래프를 통해 시각적으로 검정을 할 수도 있지만 수치적으로 검증할 수도 있다.
Breusch-Pagan 검정
통상적으로 독립변수의 값이 증가함에 따라 잔차의 변동성도 증가한다. 잔차의 제곱값 \( e^2_i \)를 종속변수로 두고 독립변수는 그대로 \( X_i \)로 하여 선형모형을 적합하는 것을 생각해볼 수 있다. 즉, 각 관측개체들에 대하여
$$ e^2_i = \gamma_0 + \gamma_1x_i, i=1,2,...,n $$
왜 갑자기 \( \gamma \)가 나오는지 모르겠다..
여기서 유의성 검정을 할 때처럼 귀무가설 \( H_0 : \gamma_1 = 0 \)을 테스트하여 기각할 수 있다면 이는 오차의 분산이 독립변수에 따라 증가 혹은 감소한다고 말할 수 있고, 즉 오차의 등분산성에 위배되는 것이 된다. 이것이 Breusch-Pagan 검정의 기본 아이디어이다.
- 귀무가설 \( H_0 = \) 등분산성을 만족한다(잔차가 동일한 분산으로 분포됨)
- 대립가설 \( H_1 = \) 이분산성을 만족한다(잔차가 동일한 분산으로 분포되지 않음)
검정의 p-값이 유의 수준(예: α = 0.05)보다 작으면 귀무 가설을 기각하고 회귀 형에 이분산성이 존재한다고 결론을 내린다.
혹은 검정 통계량을 이용할 수도 있다. Breusch-Pagan 검정 통계량 \(X^2_{BF} \)는 다음과 같다.
$$ X^2_{BF} = SSR^* \div \left ( \frac{SSE}{n} \right )^2 $$
이때,
$$ SSR^* = \sum_{i=1}^{n}\left ( \hat{\gamma_0} + \hat{\gamma_1}x_i - \overline{e^2_i} \right )^2 $$
$$ SSE = \sum_{i=1}^{n}e^2_i $$
\(X^2_{BF} \) 값이 유의미하게 크면 귀무가설을 기각하게 되고, 오차의 분포가 등분산성 가정을 위배한다고 말할 수 있다.
3. 정규성 검정
(1) Q-Q plot
관측치를 표준정규분포의 분위수와 비교하여 그리는 그래프로, 시각적으로 정규성 가정에 대한 검토를 가능하게 해준다. 모집단이 정규성 가정을 만족한다면 관측치들에 대한 Q-Q plot은 다음과 같을 것이다.
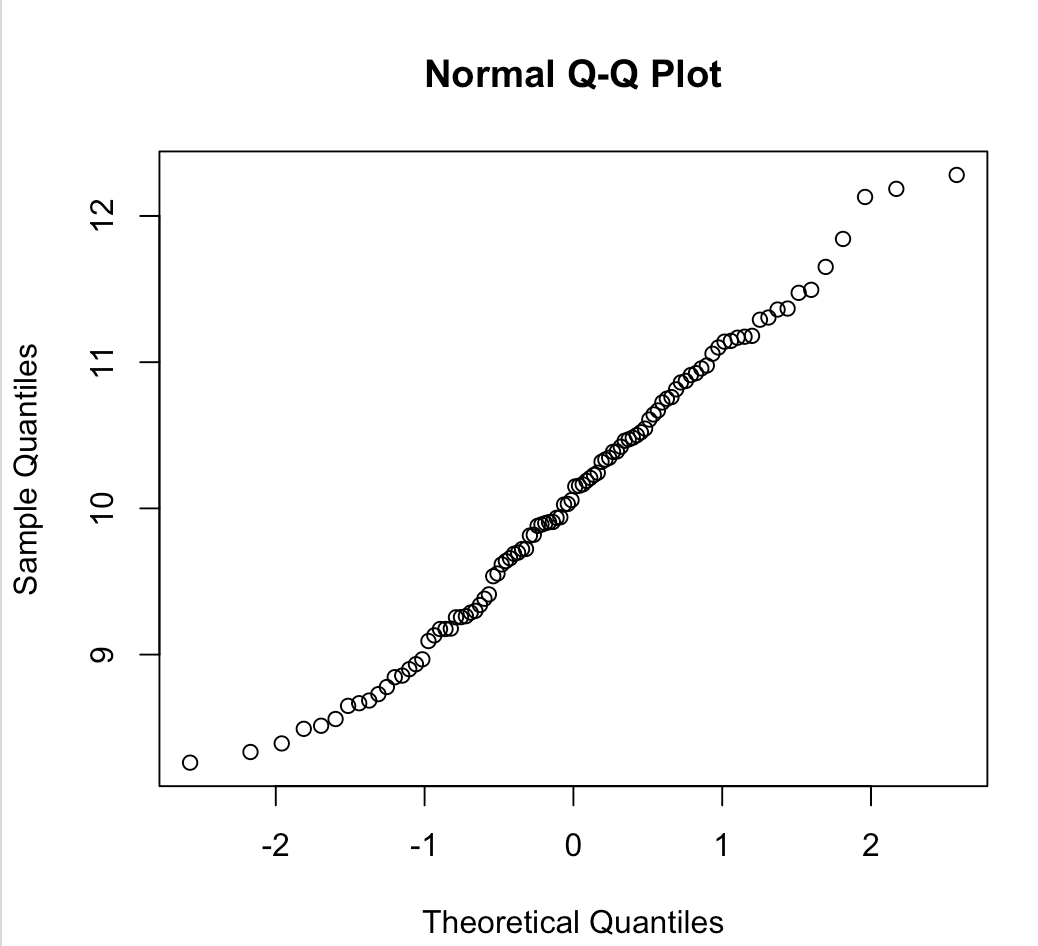
데이터의 분포가 일직선의 형태를 나타낸다.
반대로 정규성을 따르지 않는 분포의 Q-Q plot 그래프들을 다음과 같은 형태이다. 왼쪽은 카이제곱 분포이고, 오른쪽은 heavy tail 분포이다.
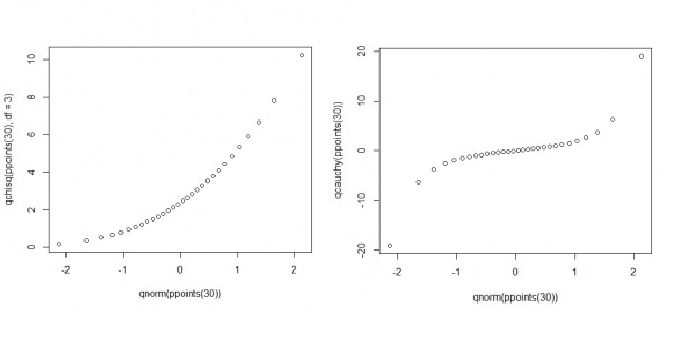
(2) Shapiro-Wilk 검정
통계량을 이용해서 수치적으로 정규성 검정을 시행할 수도 있다. Shapiro-Wilk 검정은 자료 값들과 표준정규점수와의 선형상관. 관계를 측정하여 검정하는 방법으로, 표본수가 2000개 미만인 데이터셋에 적합하다고 한다. 표본수가 2000개를 초과한다면 Kolmogorove-Smirnov 검정을 시행하는 것이 좋다.
간단히 W-통계량이라고 부르기도 하는데, Q-Q plot에서 x축과 y축을 형성하던 정규점수와 관측값의 순서통계량의 상관계수(correlation coefficient)의 제곱값이다. 이 상관계수는 W-통계량을 정의할 때 \( a_i \)로 나타낸다.
$$ W = \frac{\sum_{i=1}^n (a_ix_{(i)})^2}{\sum_{i=1}^n (x_i - \overline{x})^2} $$
이때, \( x_{(i)} \)는 i번째 순서통계량이고(표본에서 i번째로 작은 숫자), \( \overline{x} \)는 관측개체의 평균이다.
- 귀무가설 \( H_0 = \) 데이터가 정규분포를 따른다
- 대립가설 \( H_1 = \) 데이터가 정규분포를 따르지 않는다
4. 독립성 검정
Durbin-Watson 검정
Durbin-Watson 검정에 대해 설명하기 전에 우선 자기상관이란 무엇인지 이해할 필요가 있다. 선형회귀모형의 기본 가정들 중 하나는 i번째와 j번째 관측개체에 대한 오차항인 \( \varepsilon_i \)와 \( \varepsilon_j \)가 서로 상관되어 있지 않다는 것이다. 즉, 이들은 서로 독립적인 확률변량이라는 가정이다. 회귀모형에서 오차항이 가지는 의미에 비추어 볼 때 이들 사이의 상관관계의 존재는 곧 모형에 반영되지 않는 추가적 독립변수의 존재 가능성을 의미할 수도 있다. 관측값들이 얻어지는 자연스러운(natural) 순서에 따라 그들이 서로 연관되어 있을 경우 오차항(혹은 종속변수의 관측값)들이 자기상관(autocorrelation)을 가지고 있다고 한다.
Durbin-Watson 통계량은 회귀분석에서 오차항의 자기상관성 여부를 대수적 방법으로 검정하기 위해 사용되는 방법이다. Durbin-Watson 검정은 오차항들이 다음 형식의 1차의 자기상관계열을 이룬다는 가정에 근거를 두고 있다.
$$ \varepsilon_t = \rho \varepsilon_{t-1} + \omega_t, \left | \rho \right | < 1 $$
- \( \omega_t \)는 서로 독립이며, 평균이 0이고 분산이 상수인 정규분포를 따른다.
- \( \rho \)sms \( \varepsilon_t \)와 \( \varepsilon_{t-1} \)의 상관계수
Durbin-Watson 통계량 \( d \)는 다음과 같이 정의된다.
$$ d = \frac{\sum_{t=2}^n (e_t - e_{t-1})^2}{\sum_{t=1}^n e^2_t} $$
여기서 \( e_i \)는 i번째 OLS 잔차이다. 이때 통계량 \( d \)는
- 귀무가설 \( H_0 : \rho = 0 \)
- 대립가설 \( H_1 : \rho > 0 \)
에 대한 검정 통계량으로 사용될 수 있다. 왜냐하면 \( \rho = 0 \)이면, 오차들은 무상관이기 때문이다.
\( \rho \)는 알려지지 않았기 때문에, \( \hat{\rho} \)로 추정된다.
$$ \hat{\rho} = \frac{\sum_{t=2}^n e_t e_{t-1}}{\sum_{t=1}^n e^2_t} $$
'AI > Statistics' 카테고리의 다른 글
| [통계] 4가지 측정척도, Pearson correlation & Spearman rank correlation (0) | 2021.09.21 |
|---|---|
| [통계] 데이터 전처리 - 여러 가지 feature scaling 방법 (0) | 2021.09.19 |
| [통계] 정규화(Normalization) vs 표준화(Standardization) (0) | 2021.09.14 |
| [통계] F-분포와 분산 분석 ANOVA (0) | 2021.09.14 |
| [통계] 여러가지 분포 - 정규분포, 이항분포, t-분포, 카이제곱-분포 (0) | 2021.09.14 |



