회귀분석에서도 머신러닝에서도 학습에 사용할 적절한 특성을 찾는 것은 중요하다. 입력되는 데이터에서 적합한 특성을 찾는 과정을 특성 공학(feature engineering)이라고 하며, 여러 가지 특성들 중에서 학습에 필요한 특성 몇 개를 선택하기도 하고, 특성들을 조합해 새로운 특성을 만들기도 한다. 새로운 특성을 만들게 되면 데이터의 차원은 원본 특성의 수 이상으로 증가하기 쉽다. 하지만 자칫하면 모델이 더 복잡해지고 과대적합되는 결과를 불러오기도 한다. 통상적으로 새로운 특성을 추가할 때나 고차원 데이터셋을 사용할 때, 가장 유용한 특성만 선택하고 나머지는 무시해서 특성의 수를 줄이는 것이 좋다. 그래야 모델이 간단해지고, 일반화 성능도 높아지기 때문이다. 이를 위한 전략 중 하나가 일변량 통계이다.
ANOVA (analysis of variance)
일변량 통계에서는 개개의 특성과 타깃 사이에 중요한 통계적 관계가 있는지 계산하고, 깊게 관련되어 있다고 판단되는 특성을 선택한다. 분류에서는 이를 분산분석, 혹은 ANOVA라고 한다. ANOVA는 데이터를 클래스별로 나누어 평균을 비교하는 방법이다. ANOVA로 계산한 어떤 특성의 F-값이 높으면 그 특성은 클래스별 평균이 서로 다르다는 뜻이다.
이 방법의 핵심요소는 일변량, 즉 각 특성이 독립적으로 평가된다는 점이다. 따라서 다른 특성과 깊게 연관된 특성은 선택되지 않을 것이다. ANOVA는 클래스별 평균을 비교함으로써 통계적으로 깊게 연관되어 있는지(유사한지) 아닌지 알아내는데 도움이 된다.
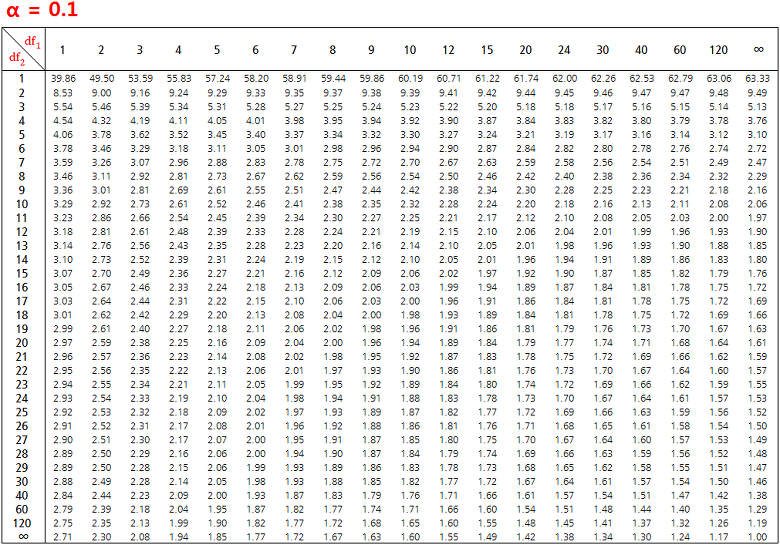
1. F-분포 (F-distribution)
우리는 이전 포스트에서 여러 가지 분포에 대해 알아보았다. t-분포를 설명하면서 F-분포를 살짝 언급하긴 했는데, F-분포란 무엇일까? F-분포는 카이제곱 분포와 같이 분산을 이용하여 추정하고 검정을 시행하기 위해 고안된 확률구조이다. 두 확률변수 \( V_1, V_2 \)가 각각 자유도 \( k_1, k_2 \)이고 서로 독립인 카이제곱 분포를 따른다고 할 때, 다음과 같이 정의되는 확률변수 F는 자유도가 \( (k_1, k_2) \)인 F-분포를 따른다고 한다.
$$ F = \frac{V_1/k_1}{V_2/k_2} \sim F(k_1, k_2) $$
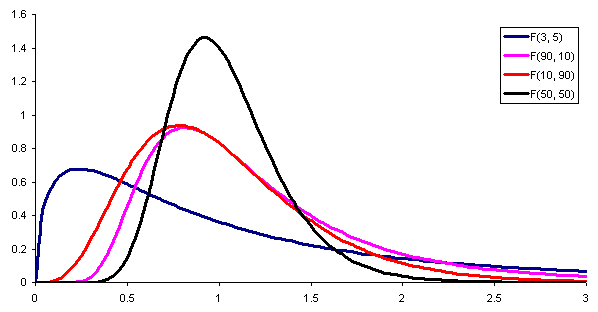
이게 무슨소리냐 하나 분명한 것은 F-분포는 카이제곱 분포 2개의 비율의 확률분포를 의미한다는 것이다. ANOVA는 두 개 이상의 다수의 집단을 서로 비교할 때 쓰는 방법이므로, F-분포도 각 집단끼리의 분산의 비교를 통해 얻어진 분포비율이 될 것이라고 역으로 생각해볼 수 있다ㅋㅋ쓰고나서도 어이없음
개체(object)로부터 얻어진 데이터들의 집합을 샘플(sample)이라고 하면, 이러한 샘플들이 2개 이상이 될 때 샘플들간의 평균의 분산을 얻을 수 있다. 이때 F-값은
$$ F = \frac{샘플간 평균 분산}{샘플 내 분산} $$
https://angeloyeo.github.io/2020/02/29/ANOVA.html -> 다음 글에서 잘 설명이 되어있는데, 결론적으로 각 집단의 평균과 표준편차를 통해 구한다. 어? 이거 어디서 많이 봤다.

MS(mean square)이란 자유도로 나눠주는 것을 말한다. 따라서 MST(mean squares treatment)는 SST의 MS, MSE(mean squares error)는 SSE의 MS를 말한다. 이때 F-값은
$$ F = \frac{MST}{MSE} $$
이다.
2. F-값과 ANOVA
다시 ANOVA 얘기로 돌아와보면, 보통 ANOVA는 세 집단을 비교할 때 많이 쓰므로, 세개의 집단이 있다고 가정할 때 ANOVA(F-검정)의 가설은 다음과 같다.
- 귀무가설 \( H_0 : \mu_1 = \mu_2 = \mu_3 \) (평균이 모두 같다)
- 대립가설 \( H_1 : \) 적어도 하나의 평균은 다르다. (평균이 다르다)
귀무가설이 옳다는 전제하에 p값이 작을수록 귀무가설을 지지하는 정도가 약해지므로 귀무가설을 기각하게 되며, 반대로 클수록 귀무가설을 지지하는 정도는 커지므로 귀무가설을 채택하게 된다.
ANOVA를 소개하면서, 'ANOVA로 계산한 어떤 특성의 F-값이 높으면 그 특성은 클래스별 평균이 서로 다르다'고 말했다. 또, 'ANOVA는 클래스별 평균을 비교함으로써 통계적으로 깊게 연관되어 있는지(유사한지) 아닌지 알아낸다'고 했다. 다시 말하면
F-값이 높다 = 집단간 평균이 서로 다르다 = 특성끼리 유사하지 않다
라는 말이 된다. 따라서 F-값이 커질수록 집단끼리의 차이는 있다고 판단되며 p값은 작아져 유의미한 결과를 보이게 된다. scikit-learn에서 ANOVA로 특성을 선택하려면 f_classif(기본값)을 선택하여 테스트하고, 계산한 p값에 기초하여 특성을 제외하는 방식을 선택한다. 이런 방식은 매우 높은 p값을 가진 특성을 제외할 수 있도록 임계값을 조정하는 매개변수를 사용한다.
3. ANOVA의 종류
종속변수의 수에 따라 ANOVA와 MANOVA로 나눌 수 있는데, 다변량 분산분석(MANOVA)는 여러 종속변수를 동시에 검정하는 반면 ANOVA는 한 번에 하나의 종속변수만 평가한다.
일원 분산분석 (one-way ANOVA)
단일 요인이 단일 반응변수에 미치는 영향을 평가 - '하나의 독립변수'와 '하나의 종속변수'

이원 분산분석, 혹은 완전 요인 분산분석 (two-way ANOVA)
두 요인이 단일 반응변수에 미치는 영향을 평가 - '두 개의 독립변수'와 '하나의 종속변수'
'AI > Statistics' 카테고리의 다른 글
| [통계] 회귀모형의 진단 (0) | 2021.09.14 |
|---|---|
| [통계] 정규화(Normalization) vs 표준화(Standardization) (0) | 2021.09.14 |
| [통계] 여러가지 분포 - 정규분포, 이항분포, t-분포, 카이제곱-분포 (0) | 2021.09.14 |
| [통계] 최대우도법(Maximum Likelihood Estimation) (1) | 2021.09.10 |
| [통계] logistic regression 예제 - 타이타닉 데이터셋 (0) | 2021.09.06 |



