Text Vectorization
어떻게 자연어를 컴퓨터에게 인식시킬 수 있을까? 컴퓨터는 모든 값을 읽을 때 0 또는 1, 즉 이진화된 값으로 받아들인다. 따라서 텍스트도 마찬가지로 수치형 텐서로 변환하는 과정이 필요한데, 자연어 처리를 위한 모델에 적용할 수 있게 언어적인 특성을 반영해서 수치화하는 것이 단어 표현(word representation) 분야이다. 다른 말로 단어 임베딩(word embedding) 또는 단어 벡터화(word vectorization)이라고 할 수 있다.
우리는 이미 [ML] 범주형 변수 처리 - Label Encoding, One-hot Encoding 포스트에서 단어를 하나의 벡터로 표현하는 방법을 공부했었다. 특히 원-핫 인코딩 방식은 단어를 표현하는 가장 기본적인 방법으로, 방법 자체가 매우 간단하고 이해하기도 쉽다. 하지만 실제로 자연어 처리 문제를 해결할 때는 잘 쓰지 않는데,
- 단어 벡터의 크기가 너무 크고 값이 희소하다 (sparsity problem)
- 단어 벡터가 단어의 의미나 특성을 전혀 표현할 수 없다
우리는 수백, 수만개의 단어와 마주하는데, 이를 원-핫 인코딩으로 벡터화한다면 아주 많은 공간을 필요로 할 것이며 0에 비해 1이 너무 작을 것이다.
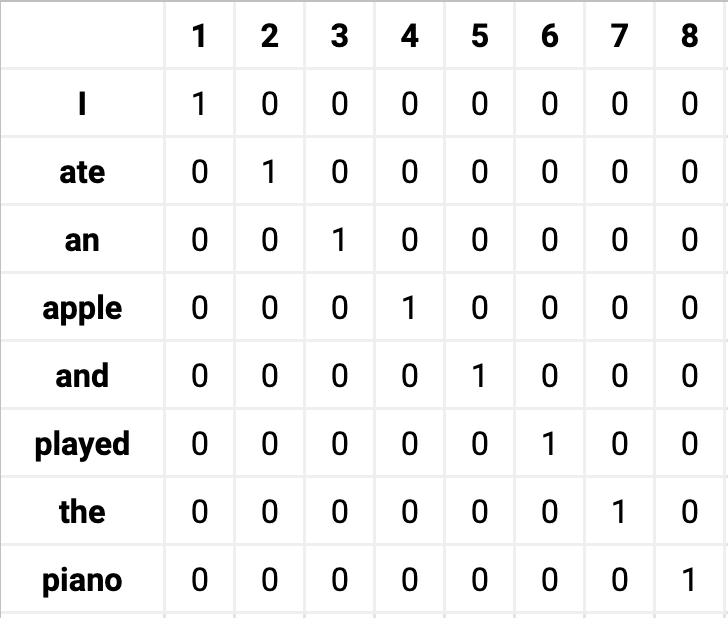
이외에 텍스트를 표현하는 간단한 방법들을 몇 가지 살펴보도록 하자.
1. BoW
BoW(Bag of Words)는 각 단어가 이 말뭉치에 있는 텍스트에 얼마나 많이 나타나는지만 헤아린다. 이 방법은 장, 문단, 소식 같은 입력 텍스트의 구조 대부분을 잃고 단어의 출현 횟수만 세기 때문에 'Bag'라는 표현을 쓴다. 출력은 각 문서에서 나타난 단어의 횟수가 담긴 하나의 벡터이다. 즉, BoW는 각 단어가 등장한 횟수를 수치화하기 때문에 이 수치 표현은 전체 데이터셋에서 고유한 각 단어를 특성으로 가진다. 원본 문자열에 있는 단어의 순서는 BoW 특성 표현에서 완전히 무시된다.
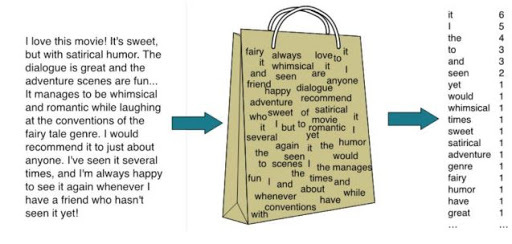
2. DTM
DTM(Document-Term Matrix)은 위 BoW의 표현 방법대로 표현하되 복수의 문서를 하나의 행렬에서 표현한 것이다. 가령 맨 왼쪽의 인덱스를 문서0, 문서1,... 이라고 했을 때, DTM을 통해 각 문서의 단어들을 하나의 행렬로 묶어서 표현할 수 있다. 행렬이 희소해진다는 원-핫 인코딩의 단점이 그대로 나타나며, (BoW도 마찬가지지만) 빈도 수로 접근하는 것의 위험성도 가지고 있다.
불용어(stopwords)란 너무 빈번하여 유용하지 않은 단어를 뜻한다. 'a'나 'the'가 많이 등장한다면 해당 문서들을 '유사하다'고 판단해도 될까? 이런 의미 없는 불용어를 잘 제거해주어야 모델 성능 향상에 도움이 된다.

3. TF-IDF
TF-IDF(term frequency-inverse document frequency, 단어빈도-역문서빈도)는 중요하지 않아 보이는 특성을 제외하는 대신, 얼마나 의미 있는 특성인지를 계산해서 스케일을 조정하는 방법이다. TF-IDF는 말뭉치의 다른 문서보다 특정 문서에 자주 나타나는 단어에 높은 가중치를 준다. 한 단어가 특정 문서에 자주 나타나고 다른 여러 문서에는 그렇지 않다면, 오히려 그 문서의 내용을 아주 잘 설명하는 단어라고 보는 것이다.
TF(단어 빈도, term frequency)는 특정한 단어가 문서 내에 얼마나 자주 등장하는지를 나타내는 값으로, 이 값이 높을수록 문서에서 중요하다고 생각할 수 있다. 하지만 단어 자체가 문서군 내에서 자주 사용 되는 경우, 이것은 그 단어가 흔하게 등장한다는 것을 의미한다. 이것을 DF(문서 빈도, document frequency)라고 하며, 이 값의 역수를 IDF(역문서 빈도, inverse document frequency)라고 한다. TF-IDF는 TF와 IDF를 곱한 값이다.
- 출처 : https://ko.wikipedia.org/wiki/Tf-idf
문서를 d, 단어를 t, 문서의 총 개수를 n이라고 표현할 때,
- \( tf(d, t) \) : 특정 문서 d에서 특정 단어 t의 등장 횟수
- \( df(t) \) : 특정 단어 t가 등장한 문서의 수
- \( idf(d, t) \) : df(t)에 반비례하는 수
$$ idf(d, t) = log(\frac{n}{1+df(t)}) $$
※ 다만 \( idf(d, t) \)의 경우 그냥 \(df(t)\)의 역수가 아닌 분모에 1을 더해주고(0이 되는 것을 방지). 로그를 취함으로써 값을 보정해준다.
여기까지 기본적인 단어 임베딩 방법을 살펴보았는데, 아직 해결되지 않은 단점이 있다. 단어의 빈도는 표현하지만 단어의 의미까지 담은 벡터라고 보기는 어려운 것이다. 따라서 벡터의 크기가 작으면서도 단어의 의미를 표현할 수 있도록 분포 가설(distributed hypothesis)을 기반으로 하는 방법들이 고안되었다.
분포 가설 (Distributed hypothesis)
단어의 분포에 관련해, 비슷한 분포의 단어나 언어 항목이 서로 유사한 의미를 지니게 되는 것을 분포 가설(distributed hypothesis)이라고 한다. "비슷한 위치에 나오는 단어는 비슷한 의미를 가진다"로 이해하면 편하다. 따라서 어떤 글에서 비슷한 위치에 존재하는 단어는 단어 간의 유사도가 높다고 판단하는 방법이다.
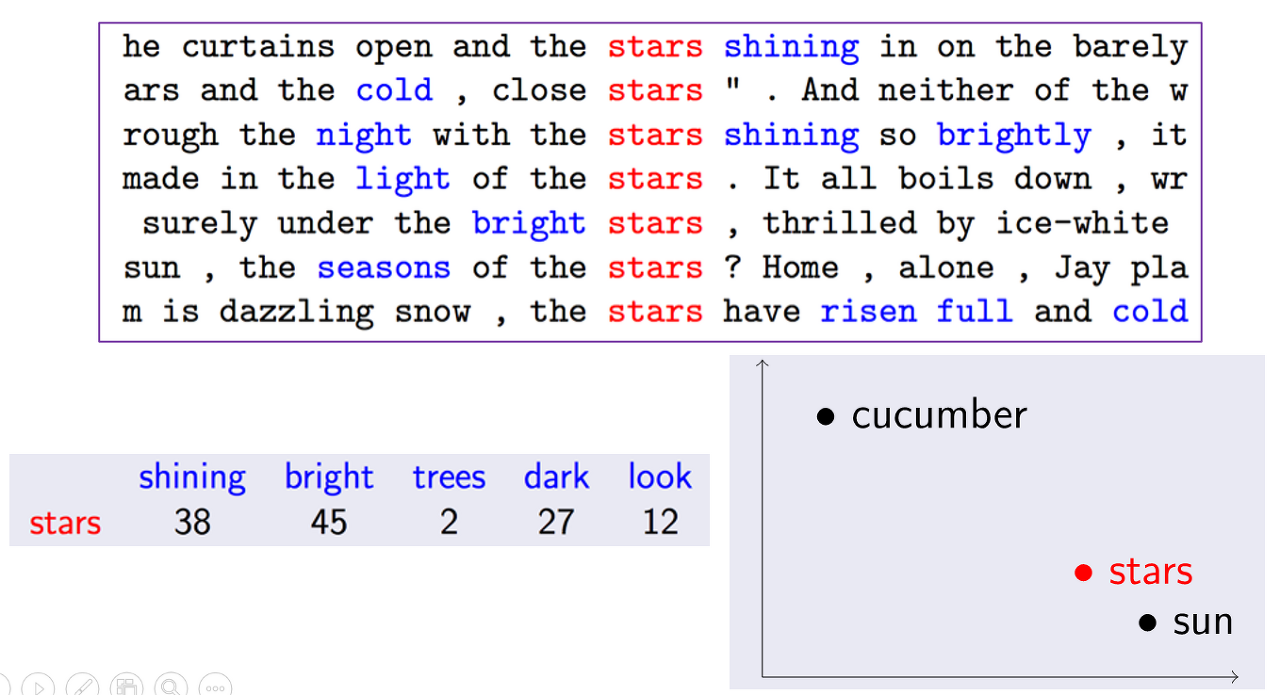
위 문장들에서 stars 단어는 shining, bright, dark 등과 같은 단어에 더 자주 포함된다. 이 단어들 모두 stars의 문맥과 의미를 이해하는 데 매우 유용하다. 이렇듯, 특정 단어의 의미를 어떻게 더 잘 표현할 수 있는지 뿐만 아니라 이 단어의 문맥에 나타날 다른 단어를 어떻게 예측하는지를 알려면 해당 단어의 분포 표현(distributional representation)을 이해해야 한다. 단어의 분포 표현은 단어를 표현할 수 있는 벡터 형태로, 원-핫 인코딩이나 그 외의 기술을 사용할 수도 있지만 유사성 측정의 중요성도 전달하는 단어의 벡터를 생성해 그 단어의 문맥상 의미를 이해할 수 있게 하는 것이 중요하다!
이는 크게 두 가지 방법으로 나눌 수 있다.
1. Count-based word embedding
특정 문맥 안에서 단어들이 동시에 등장하는 횟수를 직접 세는 방법(예: A단어, B단어 동시 등장)이다. 여기서 '동시에 등장하는 횟수'를 동시 출현(co-occurrence)라고 한다. 카운트 기반 방법은 기본적으로 co-occurrence를 하나의 행렬로 나타낸 뒤 그 행렬을 수치화해서 다시 벡터로 만드는 방법을 사용한다.

co-occurrence matrix는 단어의 수가 증가하면 증가할수록 행렬의 크기가 증가하기 때문에 매우 큰 차원을 가지게 되면서 많은 저장공간이 요구된다. 이러한 문제를 해결하기 위해 SVD를 사용하게 된다.
1-1. SVD
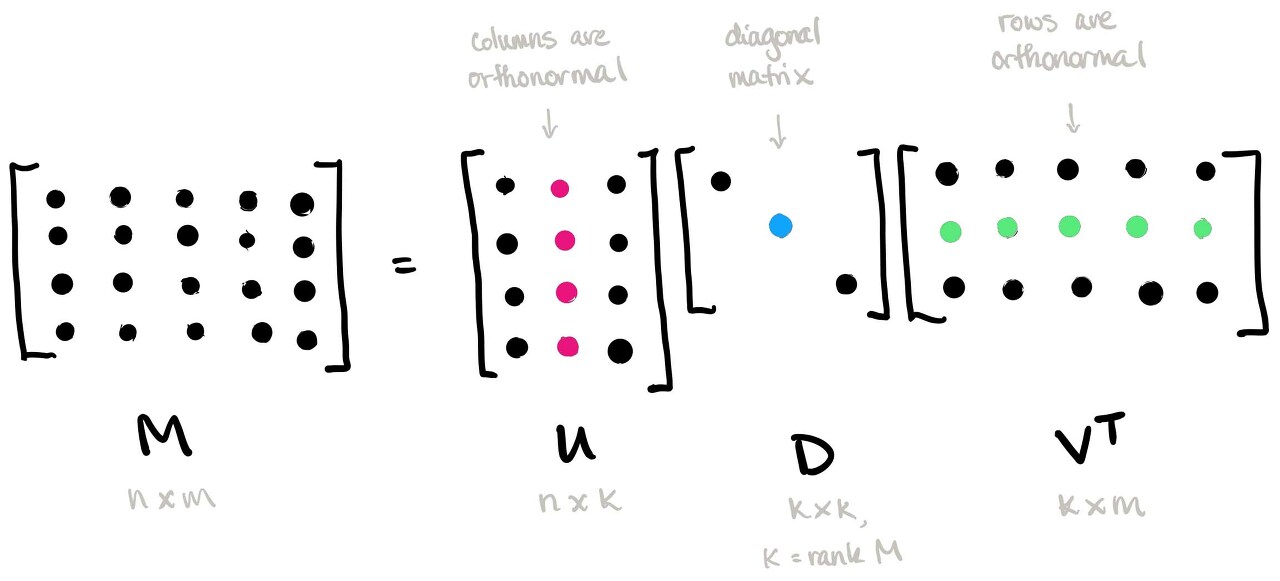
갑자기 등장하는 선형대수 SVD(Singular Value Decomposition, 특이값 분해)란 원본 행렬 \( A\)가 \(m×n\) 행렬일 때, 다음과 같이 3개의 행렬의 곱으로 분해하는 것을 말한다.
$$ A = U\Sigma V^T $$
이때 각 3개의 행렬은 다음과 같은 조건을 만족한다.
- \( U\) : \( m×m \) 직교행렬 (\(AA^T=U(\Sigma\Sigma^T)U^T\))
- \( V\) : \( n×n \) 직교행렬 (\(A^TA=V(\Sigma^T\Sigma)V^T\))
- \( \Sigma\) : \( m×n \) 직사각 대각행렬
※ 참고
- 직교 행렬(orthogonal matrix): \( n×n \) 행렬 A에 대해 \( A^TA=AA^T=I)를 만족하는, 행들이 서로 정규직교이고 열들도 서로 정규직교인 정방행렬(직교와 정규직교 정의 및 식은 https://twlab.tistory.com/37 참고)
- 대각 행렬(diagonal matrix): 주대각선을 제외한 곳의 원소가 모두 0인 행렬(직사각일 때 주의)
한편, \( \Sigma\)의 주대각 성분을 행렬 \( A\)의 특이값(singular value)라고 부른다.
특이값 분해를 이용해 \( A\)의 임의의 행렬을 여러개의 행렬로 분해하면 분해된 각 행렬의 원소의 값의 크기는 \( \Sigma\)의 값의 크기에 의해 결정된다. 즉, \( A\)를 정보량에 따라 여러 단위로 쪼개서 생각할 수 있게 한다.
Truncated SVD
truncated SVD는 full SVD에서 나온 3개의 행렬에서 일부 벡터들을 삭제시킨 것이다.

이렇게 일부 벡터들을 삭제하는 것을 "데이터의 차원을 축소시킨다"라고 하는데, 데이터의 차원을 축소하면 full SVD를 하였을 때보다 계산 비용이 낮아지는 효과가 있고, 상대적으로 중요하지 않은 정보를 삭제함으로써 설명력이 높은 정보를 남길 수 있다.
1-2. LSA (Latent Semantic Analysis, 잠재 의미 분석)
LSA는 DTM이나 TF-IDF 행렬에 truncated SVD를 사용하여 차원을 축소시키고, 단어들의 잠재적인 의미를 끌어낸다는 아이디어를 갖고 있다. 다음 포스트에서 다룰 예정인 토픽 모델링 방법의 일종으로, dimension reduction을 통해 중요한 토픽만 남기고 불필요한 토픽은 제거하는 것이다.
2. prediction-based word embedding
예측 기반방법이란 신경망 구조 혹은 어떠한 모델을 사용해 특정 문맥에서 어떤 단어가 나올지를 예측하면서 단어를 벡터로 만드는 방식이다. 알다싶이 신경망은 입력층, 은닉층, 출력층을 layer로 가지고 있으며 이들은 순전파와 역전파를 반복하며 가중치를 재조정한다. 이를 자연어 처리에서는 "코퍼스로부터 다른 문맥-대상 단어 쌍을 얻어 훈련을 계속 반복한다"로 표현할 수 있을 것이다. 이를 통해 단어 간의 관계를 학습해 코퍼스로부터 단어의 벡터 표현을 개발해낸다.
Word2vec
Word2vec은 여러 예측 기반 방법 중에서 임베딩 방법으로 가장 많이 사용되는 모델이다. Word2vec은 CBOW(Continuous Bag of Words)와 Skip-Gram이라는 두 가지 모델로 나뉜다.

두 모델은 각각 서로 반대되는 개념으로 생각하면 된다.
- CBOW : 어떤 단어를 문맥 안의 주변 단어들을 통해 예측
- Skip-Gram : 어떤 단어를 가지고 문맥 안의 주변 단어들을 예측
가령 다음과 같은 문장이 있다고 해보자.
상희는 퇴근하면서 버블티를 샀다.
CBOW는 주변 단어를 통해 하나의 단어를 예측하는 모델이므로 다음 문장의 빈칸을 채우는 것이다.
상희는 퇴근하면서 _________ 샀다.
반대로 Skip-Gram은 하나의 단어를 가지고 주변의 단어들을 예측하는 모델이다. 이런식으로 말이다.
_______ ____________ 버블티를 ____.
따라서 CBOW는 입력값으로 여러 개의 단어를 사용하고 학습을 위해 하나의 단어와 비교한다. Skip-Gram에서는 입력값이 하나의 단어를 사용하고 학습을 위해 주변의 여러 단어들과 비교한다. 그리고 학습 과정을 모두 끝낸 후 가중치 행렬의 각 행을 단어 벡터로 사용한다.
Word2vec의 두 모델은 기존의 카운트 기반 방법으로 만든 단어 벡터보다 단어 간의 유사도를 잘 측정한다는 장점이 있다. 또, 단어들의 복잡한 특징까지도 잘 잡아내며 이렇게 만들어진 단어 벡터는 서로에게 유의미한 관계를 측정할 수 있다.
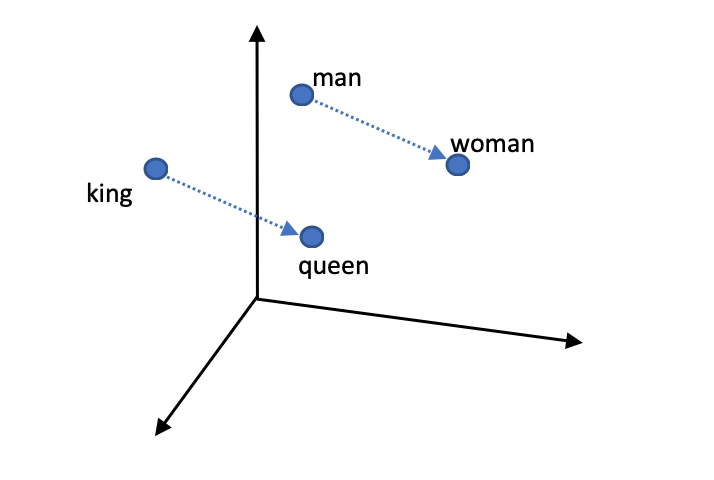
예를 들어 위 4개의 단어를 word2vec 방식을 가지고 단어 벡터로 만들었다고 하자. 이때 그림과 같이 'king'과 'queen'이라는 단어의 벡터 사이의 거리와 'man'과 'woman'이라는 단어의 벡터 사이의 거리가 같게 나온다 (cosine distance).
자료 출처: https://wikidocs.net/31698
'AI > Deep Learning' 카테고리의 다른 글
| [DL] Exploding & Vanishing Gradient 문제와 Residual Connection (0) | 2022.03.17 |
|---|---|
| [DL] Transfer Learning vs Fine-tuning, 그리고 Pre-training (0) | 2022.03.17 |
| [DL] 텍스트 데이터와 언어 모델(Language Model) (0) | 2022.03.10 |
| [DL] Attention 파헤치기 - Seq2Seq부터 Transformer까지 (2) (0) | 2022.03.08 |
| [DL] Attention 파헤치기 - Seq2Seq부터 Transformer까지 (1) (0) | 2021.11.10 |



