Residual connection은 대표적으로 컴퓨터 비전 분야에서의 ResNet 모델과 자연어 처리 분야에서의 transformer 모델에서 더 좋은 성능을 내기 위해 사용되었다. 간단히 말하자면, residual connection은 아주 deep한 신경망에서 하위 층에서 학습된 정보가 데이터 처리 과정에서 손실되는 것을 방지하기 위한 방법이다. '정보 소실'이란 무엇인지, 그리고 왜 일어나는지 이해하기 위해서는 신경망을 학습하는데 있어 고질적인 문제인 exploding gradient problem과 vanishing gradient problem에 대해 먼저 알아볼 필요가 있다.
Exploding gradient & Vanishing gradient problems
층이 많은 신경망에서 gradient problem이 일어나는 이유를 한 줄로 요약해보자면, 레이어가 많아질수록 weight value가 아주 작아지거나 아주 커지기 때문이다. 그리고 이러한 현상은 모델 파라미터가 최적해로 안정적으로 수렴하지 못하게 하는 원인이 된다.
신경망은 순전파(forward-propagation)와 역전파(back-propagation)을 반복하며 weight을 업데이트한다(자세한 내용은 [DL] 신경망의 개요 - ANN과 DNN (Neural Networks) 포스트 참고). Exploding gradient 문제를 설명하기에 앞서, hidden layer가 아주아주 많은 신경망을 상상해보자.
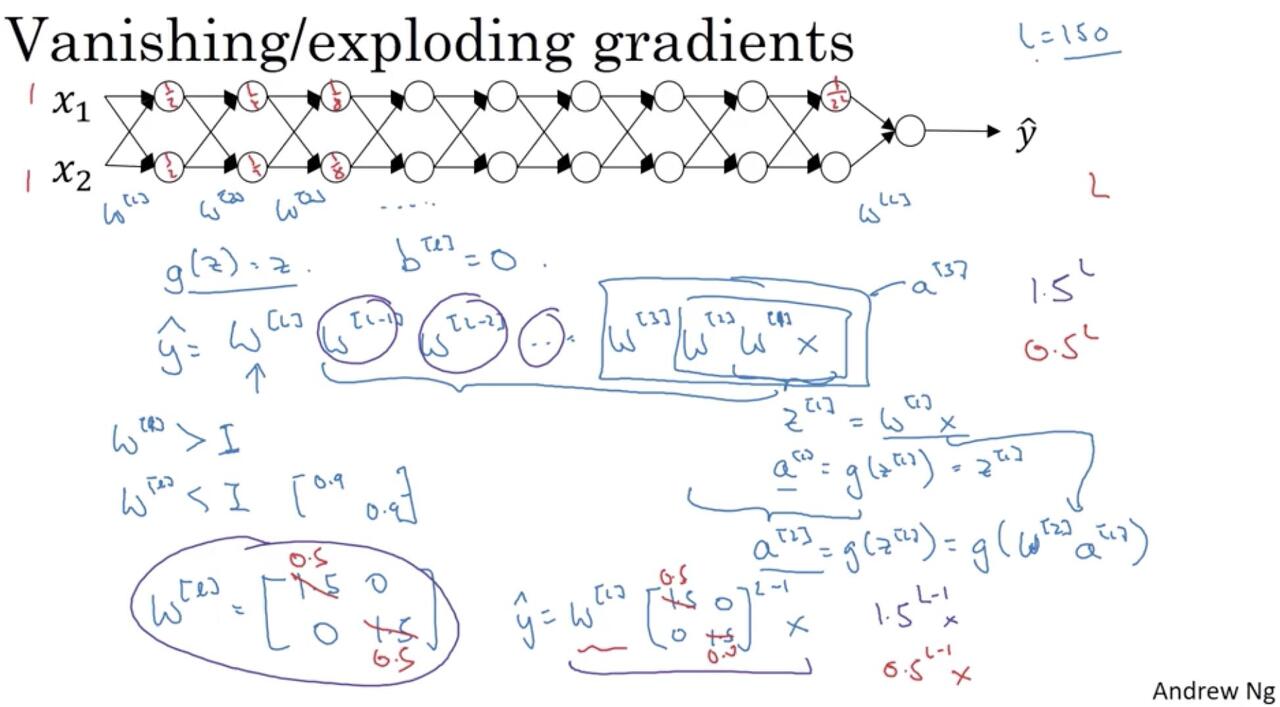
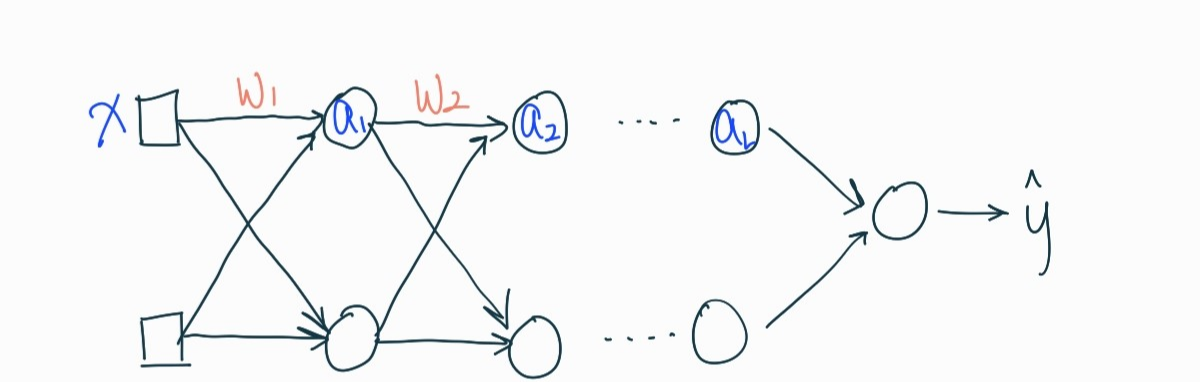
계산이 복잡해지니까 편향(bias)는 제외하고 하겠다. 그리고 활성화 함수 \(g(z) = z \)라고 가정한다. input layer의 입력값 \(x\)와 가중치 \(w_1\)을 가지고 첫 번째 hidden layer의 입력값 \(z_1\)을 계산해보면
$$ z_1 = w_1x $$
가 된다. 그 다음에 hidden layer의 활성화 함수를 거치면
$$ a_1 = g(z_1) = z_1 = w_1x $$
마찬가지로 두 번째 hidden layer까지 거치면
$$ a_2 = g(z_2) = g(w_2a_1) = w_2a_1 = w_2w_1x $$
이 된다. 보면 알지만 가중치 행렬을 \((w_1, w_2, ..., w_L)\)이라고 하면 뒤에를 그냥 \(x\)와 쭉 곱해주는 형태가 된다.
이렇게 \(a_3, a_4,....\)를 구해가다 보면 예측값인 \( \hat{y} \)를 얻게 된다. 이제 weight 행렬을 주대각선의 원소가 1보다 큰 \( w_l = \begin{bmatrix}
1.5 & 0\\
0 & 1.5
\end{bmatrix} \)이라는 단위 행렬로 둬보자. 그렇다면
$$ \hat{y} = w_L \begin{bmatrix}
1.5 & 0\\
0 & 1.5
\end{bmatrix}^{L-1} x $$
이 된다.
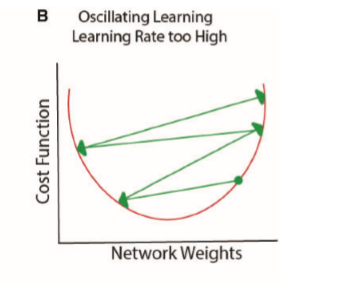
행렬의 원소 \( 1.5^{L-1} \)은 \( L\)의 값이 커질수록 기하급수적으로 상승한다(당장 \(L-1=20\)만 돼도 3,000이 넘는다). 여기서 \( L \)은 hidden layer의 개수만큼 커지므로 마지막 \( \hat{y} \) 또한 아주아주 큰 값이 된다. 이제 실제값 \(y\)와의 차이를 모두 더한 \(E_{total}\)을 통해 역전파를 수행해보자. gradient는 \( \gamma\frac{\partial E_{total}}{\partial w_L} \)인데(경사하강법 식은 위키독스 참고) 이미 실제값과 예측값의 차이가 큰 상황에서 gradient를 계산봤자 크다. 이렇게 계속 input layer 쪽으로 연쇄적으로 역전파를 해봐도 최적의 weight로 업데이트 해나가는 데는 별로 도움이 안된다. 말하자면 아래와 같이 수렴하지 못하는 모양이 된다. 이것이 exploding gradient problem이다.
반대로 weight 행렬을 1보다 작은 수인 weight 행렬 \( w_l = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \)로 둬보자. 마찬가지로
$$ \hat{y} = w_L \begin{bmatrix} 0.5 & 0\\ 0 & 0.5 \end{bmatrix}^{L-1} x $$
가 되는데 \( 0.5^{L-1} \)은 아주아주 작을 것이다(0에 가까워진다). 마찬가지로 gradient도 아주아주 작다. 기존의 weight에서 gradient를 빼서 weight을 갱신해봤자 근소한 차이일 뿐이다. 여기다 심지어 학습률조차 작다(보통은 소수점 셋째자리의 작은 양수). 이렇게 되면 수렴하기까지 오랜 시간이 걸리거나, 위와 마찬가지로 수렴이 잘 안된다. 이러한 현상을 vanishing gradient problem이라고 한다.
Residual Connection
그럼 깊는 신경망은 어떻게 잘 학습시킬 수 있을까? Residual connection은 일부 레이어를 건너뛰어 데이터가 신경망 구조의 후반부에 도달하는 또 다른 경로를 제공함으로써 gradient가 계속 커지거나 작아지는 문제를 해결한다.
레이어 \(i \)에서 레이어 \(i + n\)까지의 일련의 레이어와, 이들 레이어에 의해 표현되는 함수를 \(F\)로 둬보자. 레이어 \( i\)로 들어오는 입력값을 \(x\)라고 했을 때, 전통적인 피드포워드(feed forward) 네트워크에서는 \( x\)가 레이어를 순차적으로 지나며 레이어 \( i+n \)의 output은 \(F(x)\)가 될 것이다. 하지만 몇개의 레이어를 bypass하는 residual connection은 아래와 같이 작용한다.
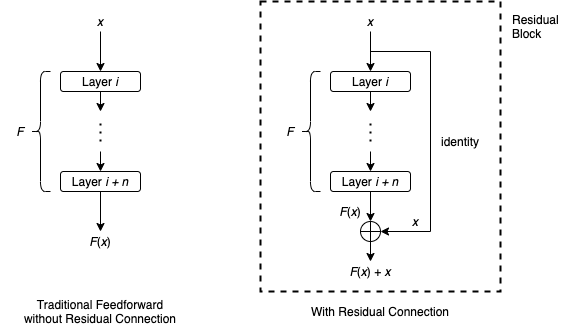
즉, 레이어 \( i \)를 통과하기 전 입력값 \( x\)를 그대로 들고와 최종 output에 더해주는 \(F(x) +x\)의 형태가 되는 것이다. 입력 \(x\)를 취하여 출력 \(F(x) + x\)를 생성하는 전체 구조를 보통 residual block이라고 한다. 대부분의 경우 residual block은 \(F(x) + x\)에 적용되는 ReLU와 같은 활성화 함수를 포함한다.
수백 개의 레이어가 있어도, residual block이 포함된 신경망은 경험적으로 훨씬 더 용이하게 수렴하는 것을 나타내고 있다(손실되거나 폭주하는 gradient값에 대한 보정으로 받아들이면 될듯... 맞나??). ResNet은 이전 모델인 VGG에 비해 더 많은 레이어를 가진 모델이고 이러한 방식이 성능 개선에 도움이 되었다고 한다.
How does it help training deep neural networks?
For feedforward neural networks, training a deep network is usually very difficult, due to problems such as exploding gradients and vanishing gradients. On the other hand, the training process of a neural network with residual connections is empirically shown to converge much more easily, even if the network has several hundreds layers. Like many techniques in deep learning, we still do not fully understand all the details about residual connection. However, we do have some interesting theories that are supported by strong experimental results.
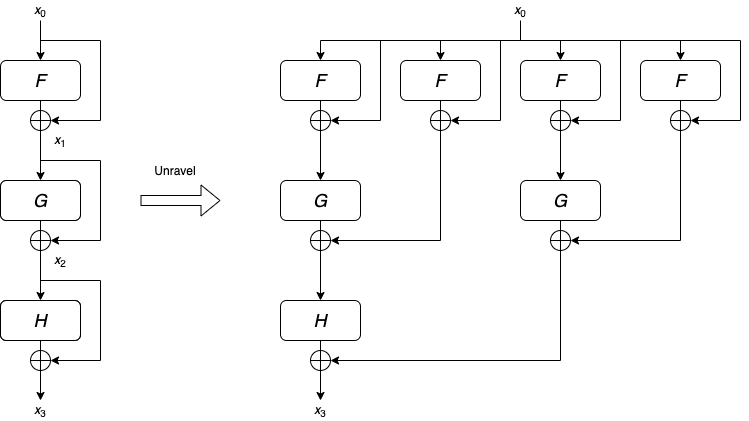
Behaving Like Ensembles of Shallow Neural Networks
For feedforward neural networks, as we have mentioned above, the input will go through each layer of the network sequentially. More technically speaking, the input goes through a single path that has length equal to the number of layers. On the other hand, networks with residual connections consist of many paths of varying lengths.
- 출처 : https://towardsdatascience.com/what-is-residual-connection-efb07cab0d55
gradient problems에 대한 설명은 앤드류 응 교수님 강의 참고! 나 이분 없으면 공부못해...
'AI > Deep Learning' 카테고리의 다른 글
| [DL] keyword extraction with KeyBERT - 개요 및 알고리즘 (0) | 2022.03.28 |
|---|---|
| [DL] Topic modeling with BERTopic - 개요 및 알고리즘 (0) | 2022.03.27 |
| [DL] Transfer Learning vs Fine-tuning, 그리고 Pre-training (0) | 2022.03.17 |
| [DL] 자연어 처리에서의 텍스트 표현 - 단어 임베딩(Word Embedding) (0) | 2022.03.11 |
| [DL] 텍스트 데이터와 언어 모델(Language Model) (0) | 2022.03.10 |



