[ML] 토픽 모델링(Topic Modeling) - LSA와 LDA 포스트에서 LDA의 가정과 원리에 대해 간단히 설명해본 적이 있다. 좋은 기회가 있어서 논문을 읽게 되어 더 자세하게 설명을 해보려 한다. 토픽 모델링에 대한 설명은 위 포스트를 참고, 이번 포스트는 LDA의 generative model과 inference과정에 초점을 맞춰보려 한다.
LDA 논문 원본 https://www.jmlr.org/papers/volume3/blei03a/blei03a.pdf 이쪽!
Terminology
본격적으로 들어가기 앞서 각 term에 대한 정의를 살펴본다.
- 단어(word)란 이산 데이터의 기본 단위이며, \( {1, ..., V} \)의 형식으로 index된 어휘(vocabulary)의 항목으로 정의된다.
- 문서(document)란 \( N\)개의 단어들로 표현되는 시퀀스이다; \( w=(w_1, w_2, ..., w_N) \). \( w_n\)은 문서 안에서 \(n\)번째 단어이다.
- 코퍼스(corpus)란 \(M\)개의 문서의 집합이다. \(D = \left\{ w_1, w_2, ..., w_M\right\} \)
1. Generative Probabilistic Model
LDA는 코퍼스의 생성 확률론적 모델(generative probabilistic model)이다. Generative model은 \(x\)를 분류하는 데 있어 \(x \)가 어느 \( y\) 분포에서 왔는지 파악하는 것에부터 출발한다.

\( x = (1, 4, 5, 6, 9) \)라는 5개의 새로운 데이터를 얻었다고 해보자. 이렇게 새로운 \(x\)가 나타났을 때, 어떤 \(y\)에 배정해야 더 likely할까? Generative model은 어떤 데이터의 분포를 만들고, 그 분포에서의 확률을 maximize하는 방향으로 분류를 하게 된다.
generative model은 레이블 되지 않은 데이터가 출현했을 경우를 포함하여 분포를 추청하는 것에 집중한다.
LDA는 분포와 관련된 중요한 가정 두 가지를 base로 한다.
- 문서는 토픽 분포에 대한 무작위 혼합(random mixture)으로 표현되며,
- 각 토픽은 단어에 대한 분포로 이루어져 있다.

노란색 토픽은 gene, dna, genetic,..과 같이 토픽에 해당하는 단어들과, 각각의 단어가 토픽에 나타날 확률로 형성되어 있다. 그러니까 해당 토픽은 등장하는 단어들에 대한 확률분포로 나타낼 수 있을 것이다(등장하는 단어들로 미루어 보았을 때 토픽명을 '유전학'이라고 붙일 수 있을 것이다). 오른쪽의 문서를 보면 파란색, 빨간색 토픽에 해당하는 단어보다는 노란색 토픽에 해당하는 단어들이 많다. 따라서 위 문서의 메인 주제는 노란색 토픽(유전학)일 가능성이 크다.
LDA는 코퍼스 \(D \)에서 다음과 같은 과정으로 문서 \( w\)를 생성한다고 가정한다:
1-1. Choose \( N \sim Poisson(\zeta ) \).
단어의 개수 \( N\)은 포아송 분포에서 기인한다. 그런데 현실에서 따져보면 책 하나의 페이지수나 그 페이지에 등장하는 단어의 수가 모두 제각각이기 때문에, \(N\)을 하나의 값으로 고정할 필요는 없다(생략 가능).
Finally, the Poisson assumption is not critical to anything that follows and more realistic document length distributions can be used as needed.
1-2. Choose \( \Theta \sim Dir(\alpha) \).
- \(\Theta \): 토픽 비중(topic mixture)
- \(\alpha \): 디리클레 파라미터
\( \Theta \)는 여러개의 토픽 분포를 합쳐 놓은 mixture model이다. Mixture model이란, 여러 개의 하위 분포들이 섞여서 만든 하나의 큰 분포를 말한다. 위에서 말했듯이, LDA는 하나의 문서가 여러 개의 토픽으로 이루어져 있다고 가정하기 때문에, 여러 토픽 분포들이 합쳐진 하나의 혼합물로 이해할 수 있다.

그리고 이 mixture model \( \Theta \)는 디리클레 분포를 따른다.
디리클레 분포(Dirichlet distribution)은 베타 분포의 확장이다. 베타분포의 확률변수가 0과 1사이의 실수값을 갖는다면, 디리클레 분포는 합이 1인 k차원의 다항확률변수에 대해 모델링한 것이라고 할 수 있다.
예를 들어, \( \Theta = (0.7, 0.15, 0.15) \)일때 \( k=3 \), 즉 '3개의 토픽에 대한 확률분포(prior)를 디리클레 분포로부터 가져온다'라는 뜻은 mixture model에서 각 분포가 선택될 확률이 0.7, 0.15, 0.15라는 것이다.

그렇다면 이 \( \Theta \)가 sampling되는 디리클레 분포는 어떻게 생겼을까? 그것은 \( \alpha \)값에 따라 다르다.

보통 \( \alpha \)가 클수록 각 토픽분포가 뽑힐 확률이 균등해진다. 반대로 \( \alpha \)가 작을수록 특정한 토픽분포가 뽑힐 확률이 높아진다. (이걸 직관적으로 이해하자면 위의 그림을 봤을 때 \( \alpha \)가 1일 때는 삼각형의 edge에 가깝고, 반대로 2나 10으로 커질수록 삼각형의 안쪽(?)으로 밀집되는 경향이 있다. 각 모서리를 토픽이라고 생각한다면 쉬울 거 같음)
1-3. For each of the N words \(w_n \):
(a) Choose a topic \(z_n \sim Multinomial(\Theta) \).
위의 과정까지 해서 \( \Theta \)를 sampling 했으니, 이제 그 값에 맞춰 토픽을 고른다. 만약 Topic 1, 2, 3이 있고 \( \Theta = (0.7, 0.15, 0.15) \)라면, \(z_n = 1\)이 될 것이다.
- \( z_n \): \( n\)번째 단어에 대한 토픽 변수
(b) Choose a word \(w_n \) from \( p(w_n|z_n, \beta) \), a multinomial probability conditioned on the topic \( z_n \).
토픽을 골랐으면 이제 해당 토픽에서 가장 등장할 확률이 높은 단어를 뽑는다. 이것을 실행하려면 각 토픽들에 대한 단어의 분포가 형성되어 있어야 하는데, 다음과 같은 topic-word 행렬로 단어의 출현 빈도수를 정리한다.

그런데 알다싶이 이런 빈도표는 매우 sparse할 것이다(자주 나오는 단어보단 한 번 나오고 안나오는 단어들이 더 많을 것이다). 이를 보정하기 위해서 이 행렬을 디리클레 분포로 만들어버리고, 이 디리클레 분포의 하이퍼파라미터를 \( \beta \)로 지정한다. ??????
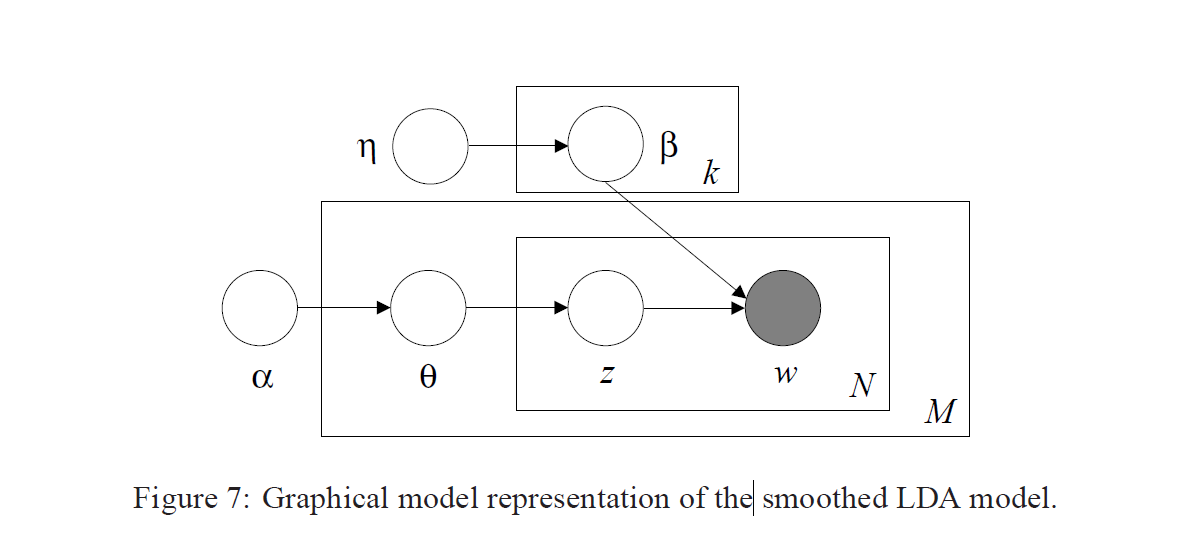
Generation model의 5줄 요약:
1. 우선 생성할 단어의 총 개수 N을 포아송 분포에서 추출하고
2. 디리클레 분포를 통해 토픽 분포 \( \Theta \)를 추출하고
3. N개의 단어 \(w_n\)에 대해 다음을 반복 수행:
- \( \Theta \)를 기반으로 하위 분포, 즉 토픽 하나를 선정한 다음(\( z_n \))
- 이 토픽에 기반해서 단어를 하나 선정한다.
결론적으로, \(\alpha \)와 \(\beta \)가 주어졌을 때 \( p(\Theta, z, w | \alpha, \beta) \)는 다음과 같이 구할 수 있다.
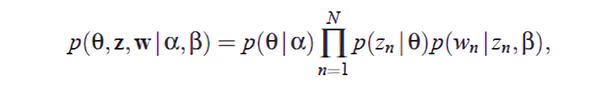
2. Inference
Generative model을 기반으로 코퍼스에서부터 토픽과 단어가 어떻게 생성되는지 봤으니, 이제 반대로 단어로부터 토픽을 어떻게 뽑아낼 수 있는지 보자.
'LDA를 통해 토픽 모델링을 하려고 한다'는 말은 직접적으로 관찰할 수 있는 값(단어 \(w\))와 고정된 값(\( \alpha \)와 \( \beta \))를 통해 토픽과 관련된 변수(\( \Theta\)와 \(z\))를 구하려고 한다는 뜻이다.
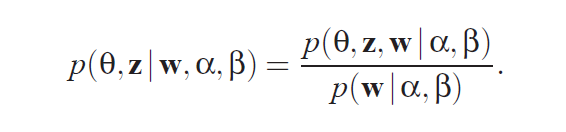
그런데 이 결합확률은 계산이 불가능하다. 정확히 말하면 단어가 늘어나면 늘어날수록 computation이 기하급수적으로 증가해 intractable하다고 한다. 따라서 논문에서는 simple convexity-based variational algorithm을 통해 LDA inference를 수행하는데, 대부분의 블로그에서는 깁스 샘플링(gibbs sampling)으로 설명을 해놨기 때문에 이를 차용하려고 한다.
The key inferential problem that we need to solve in order to use LDA is that of computing the posterior distribution of the hidden variables given a document. Unfortunately, this distribution is intractable to compute in general. Indeed, to normalize the distribution we marginalize over the hidden variables.
LDA에서는 나머지 변수를 고정시킨채 한 변수만을 변화시키면서 불필요한 일부 변수를 sampling에서 제외하는 collapsed gibbs sampling을 쓴다. 깁스 샘플링을 이용해서 \(z\)를 구하는 과정에서 \( \Theta \)를 간접적으로 구할 수 있다. 마찬가지로 위에서 \( p(\Theta, z, w | \alpha, \beta) \)를 계산할 때, \(z\)로 \( \Theta\)와 \( w\)를 구할 수 있어 나머지 두 변수를 고려할 필요가 없어진다.
LDA의 깁스 샘플링 수식은 다음과 같다.
$$ p(z_i = j | z_{-i}, w) $$
샘플링 순서를 간단히 소개해보자면
1. 단어를 토픽에 무작위로 assign
2. masking을 통해 document-topic 분포 계산
3. masking을 통해 word-topic 분포 계산
4. 2와 3을 곱해 그 크기로 토픽 도출
자세한 방법은 이 포스트에 소개되어 있다. 어쨋든 실제 계산식은 다음과 같다.
$$ p(z_{d, i}=j|z_{-i}, w) = \frac{n_{d, k}+\alpha_j}{\sum_{i=1}^K (n{d, i}+\alpha_i)} \times \frac{v_{k, w_{d,n}}+\beta_{w_{d,n}}}{\sum_{j=1}^V(v_{k,j}+\beta_j)} = AB $$

이런 식으로 모든 문서와 단어에 대해 깁스 샘플링을 수행하면 모든 단어마다 토픽을 할당해줄 수 있게 된다. 보통 1000회~1만회 정도 반복 수행하면 그 결과가 수렴한다고 한다.



