ViT 논문 리뷰 포스트에 이어 트랜스포머를 이용해 image recognition task를 수행하는 딥러닝 모델들에 대해 계속 다뤄보려한다. 이번 주제는 Swin Transformer로, 2021년 3월 마이크로소프트(Microsoft Research Asia)에서 발표하였다. 논문은 이쪽에서 확인할 수 있다.
1. ViT to Swin
논문의 introduction 부분에서 저자는 기존의 비전 분야에 대한 Transformer based approach가 어떤 문제점을 가지고 있는지 언급한다. 골자는 'computational complexity on high-resolution images'로 축약할 수 있는데, 이미지의 해상도, 그러니까 픽셀이 늘어나면 늘어날수록 모든 patch의 조합에 대해 self-attention을 수행하는 것은 불가능해진다는 것이다.
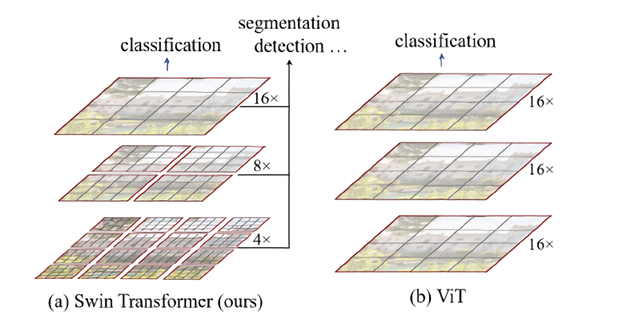
Swin transformer는 hierarchical feature map을 구성함으로써 이미지 크기에 대해 linear complexity를 가질 수 있도록 고안된 아키텍처를 가진다. 이러한 장점은 Swin Transformer가 다양한 비전 분야의 작업에 있어 general-purpose backbone으로 적합하게 만들며, 단일 해상도의 feature map을 만들고 quadratic complexity를 갖는 이전의 트랜스포머 기반 아키텍처와 차이점을 가진다.
2. Distinct features
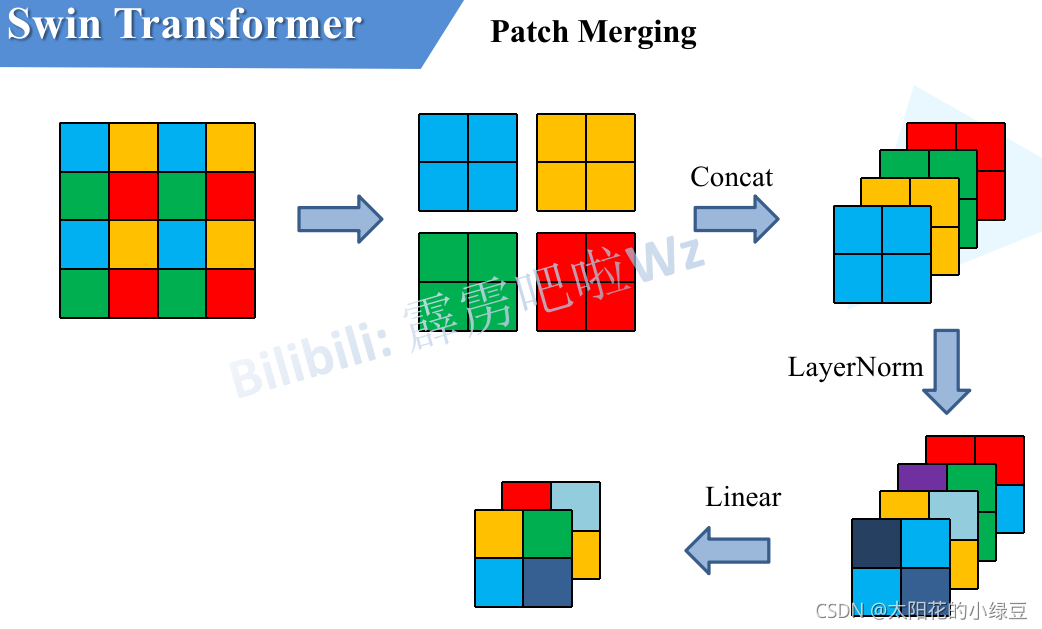
논문명인 'Swin Transformer: Hierarchical Vision Transformer using Shifted Windows'에서 본 모델이 가지는 특징 키워드를 두 가지 뽑자면 Shifted Windows와 Hierarchical이 될 것이다. ViT가 이미지를 작은 patch들로 쪼개는(image->patch) 방향으로 간다면, Swin transformer은 그보다 더 작은 단위의 patch로부터 시작해서 점점 patch들을 merge해나가는 방식을 취한다(patch->proportion of image->image). patch들을 합치며 계층적인 구조로 각 단계마다 representation을 갖기 때문에 다양한 크기의 entity를 다루어야 하는 비전 분야에서 좋은 성능을 낼 수 있는 것이다.
또, shifted window partitioning는 이전 레이어의 window와 현재의 window 사이를 이어주며 모델의 성능을 효과적으로 향상시킨다. 여기서 window란 \( M\)개의 인접한 patch들로 구성되어 있는 patch set이다. Swin transformer는 위에서 제시한 computational complexity의 한계를 극복하기 위해 window들 내부에서만 patch끼리의 self-attention을 계산하는 것으로 제안한다. 하지만 단순히 window 기준으로 나누면 각 window의 경계 근처 patch(정확히는 픽셀)들은 인접해 있음에도 self-attention 계산이 수행되지 않는데, 레이어 \( l \)의 분할이 발생한 patch에서 \( (\left \lfloor \frac{M}{2}, \frac{M}{2} \right \rfloor) \)칸 떨어진 patch에서 레이어 \(l+1\)의 window 분할함으로써 window 간의 연결성을 반영한다. 그리고 self-attention 계산이 \(M\)개의 patch들로만 제한되기 때문에 연산의 효율성도 획득할 수 있게 된다.
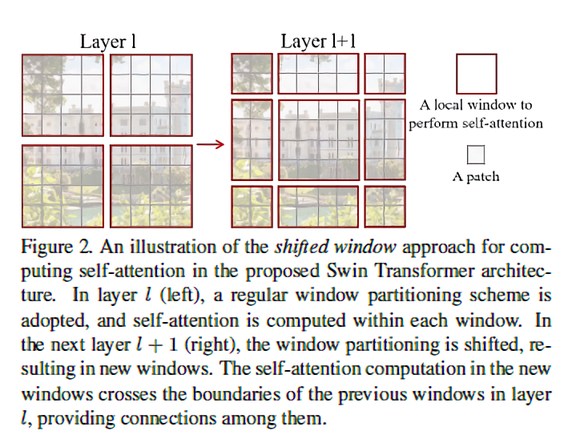
참고로 두 window 분할 방식은 Swin transformer에서 모두 쓰이니 terminology를 알아두면 좋다!
- W-MSA: feature map을 \(M \)개의 window로 나누는 것 (regular - 위 그림에서 왼쪽)
- SW-MSA: W-MSA 모듈에서 발생한 패치로부터 \( (\left \lfloor \frac{M}{2}, \frac{M}{2} \right \rfloor) \)칸 떨어진 patch에서 window 분할 (shifted - 위 그림에서 오른쪽)
3. Architecture
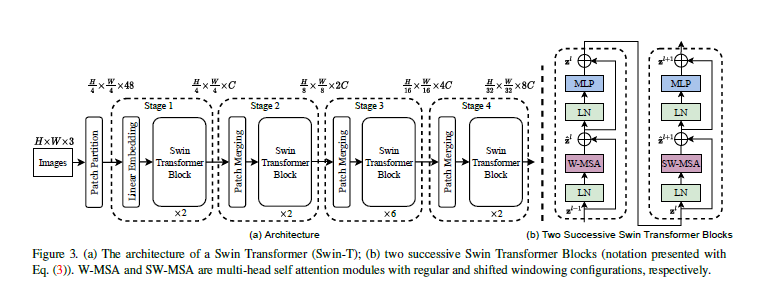
- \(H\) / \(W\): 이미지의 높이와 넓이
- \(C\): arbitrary dimension size for an image token (implemented as \(C=4\))
3-1. Relative position bias
아마 가장 먼저 보이는 것은 position embedding이 없다는 점일 것이다(필자가 그랬어서 이 내용을 맨 앞에 가져왔다ㅎ). ViT에서는 각 이미지 토큰의 위치 정보를 보존하기 위해 position embedding을 더해주었다. 반면, Swin transformer는 이러한 과정이 없고, self-attention을 수행하는 과정에서 relative position bias를 추가해준다.
$$ Attention(Q, K, V) = SoftMax(QK^T/\sqrt{d}+B)V $$
위의 식을 보면 일반적인 attention score 구하는 식 뒤에 bias인 \(B\)를 더해준다(\(d\)는 query/key dimension). \(M\)개의 patch가 하나의 window를 구성하므로 각 축을 따라 상대적인 위치는 \( [-M+1, M-1] \)의 범위 안에 있다. 따라서 작은 크기의 bias 행렬을 \( \hat{B}\in \mathbb{R}^{(2M-1) \times (2M-1)} \)에 속하는 \(B\)로 파라미터화 할 수 있다.
이는 기존의 positional embedding이 절대좌표를 더해주는 식이었던 것에 반해(absolute position embedding) 위치는 상대적이라는 개념을 적용한 relative position representation이라고 할 수 있다. 논문에 따르면 이 bias 항이 없거나 absolute position embedding을 사용했을 때보다 상당한 모델 성능의 향상을 보였다고 한다.
3-2. Patch partition
ViT와 같은 patch 분리 모듈을 통해 raw input인 RGB 이미지를 겹치지 않는 patch들로 쪼갠다. 마찬가지로 patch는 일종의 토큰으로 취급되며, 논문에서는 patch size를 \( (4 \times 4) \)로 잡았으므로 하나의 feature는 \( (4 \times 4 \times 3)=48 \)의 shape을 가진다.
3-3. Stages
Swin Transformer block
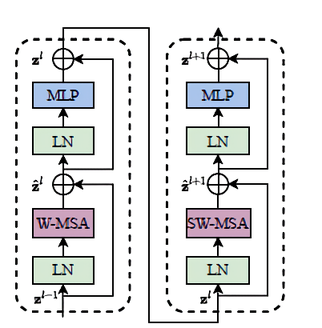
Swin transformer의 트랜스포머 block은 multi-head self-attention(MSA) 모듈을 window 기반의 W-MSA와 SW-MSA 모듈로 교체하였으며, 각각의 MSA 모듈을 포함한 2개의 연속적인 트랜스포머로 하나의 Swin block이 형성된다. 다른 레이어는 기존의 ViT와 동일하다. window 기반의 MSA 모듈 이후에는 GELU 활성화 함수를 사이에 둔 2층 linear layer로 구성된 MLP block이 배치되었다. 각 MSA 모듈과 MLP 앞에 LN(Layer Norm) 층이 적용되고, 각 모듈 뒤에 residual connection이 적용된다.
위에서 언급했지만, 표준 트랜스포머 아키텍처와 image classification을 위한 adaptation은 둘 다 토큰과 다른 모든 토큰 사이의 관계를 계산하는 global self-attention을 수행한다. 이러한 global computation은 토큰 수에 비례해 quadratic complexity를 가지게 되고, 고해상도 이미지를 나타내기 위해 엄창난 토큰 set을 필요로 하는 많은 비전 문제에 적합하지 않다. Swin transformer는 효율적인 모델링을 위해, local window 내에서만 self-attention을 계산할 것을 제안한다. window는 겹치지 않는 방식으로 이미지를 균등하게 분할할 수 있도록 배열되어 있다(self-attention in non-overlapped windows). 각 window에 \( M \times M \) patch들이 포함되어 있다고 가정하면, global MSA 모듈의 computational complexity와 \( h \times w \) 크기의 patch를 기반으로 하는 window는 다음과 같다:
\begin{align} \Omega (MSA) = 4hwC^2 + 2(hw)^2C \\ \Omega (W-MSA) = 4hwC^2 + 2M^2hwC \end{align}
여기서 전자는 patch에 대해 quadratic하고, 후자는 \(M\)이 고정될 때 linear하다(논문에서는 \(M=7\)로 설정).
다만 shifting을 적용함에 있어 효율적으로 window를 배치해야할 필요성이 있는데, W-MSA에서 \( \left \lceil \frac{h}{m} \right \rceil \times \left \lceil \frac{w}{m} \right \rceil \) 였던 window 수가 SW-MSA 모듈에서는 \( (\left \lceil \frac{h}{m} \right \rceil + 1) \times (\left \lceil \frac{w}{m} \right \rceil + 1) \)로 달라지게 된다(보다 편한 이해를 위해, [2]Distinct features 문단의 두 번째 사진을 revisit해보면 W-MSA에서 \( (2 \times 2) \)였던 window의 개수가 SW-MSA에 와서는 \( (3 \times 3) \)로 늘어났을 뿐만 아니라 크기가 \(M \times M\)보다 작은 window들이 생긴 것을 확인할 수 있다). 따라서 논문에서는 이를 해결하기 위한 두 가지 approach를 제시한다.
- naive solution: 작아진 window들에 padding을 두어 크기를 다시 \( M \times M \)으로 맞춰주고, attention을 계산할 때 padding된 값들을 마스킹 해준다. 하지만 window의 수는 여전히 늘어나게 되기 때문에 이러한 naive 접근으로 증가한 computation은 상당하다(\( (2 \times 2) \) -> \( (3 \times 3) \), 2.25배 더 큼)
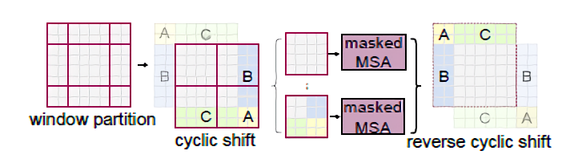
- efficient batch computation for shifted configuration: 왼쪽 상단을 향해 cyclic하게 회전하기. shift 이후 배치 window는 feature map에서 인접하지 않은 여러 하위 window로 구성될 수 있으므로, self-attention 계산을 각 하위 window 내에서 제한하기 위해 마스킹 메커니즘이 사용된다. cyclic-shift를 사용하면 배치 window 개수가 regular window partitioning 때와 동일하게 유지되므로 효율적이다(low latency).
[Stage 1]
Linear embedding을 거쳐 \(C\)차원으로 사영된다. (\( \frac{H}{4} \times \frac{W}{4} \times 48\) to \( \frac{H}{4} \times \frac{W}{4} \times C\))
이렇게 형성된 patch 토큰들은 Swin Transformer block을 통과하게 된다.
[Stage 2]
계층적인 구조를 갖는 feature map을 생성하기 위해 patch merging 단계를 거친다. 여기에서는 인접한 \( (2 \times 2) =4\)개의 patch들끼리 결합하여 하나의 큰 patch를 새롭게 만든다. patch를 합치는 과정에서 차원이 \( 4C\)로 늘어나기 때문에 linear layer를 통과하여 \(2C \)로 조정한다(feature transformation). 그리고 다시 Swin transformer block을 통과하며 self-attention 계산을 마친다.
[Stage 3&4]
Stage 2를 거치며 나온 output은 \( \frac{H}{8} \times \frac{W}{8} \times 2C\)가 된다. 즉, patch size는 점점 커지고 수도 많아지며 각 토큰의 차원은 두 배씩 늘어간다. 이 절차는 Stage 3와 4에 걸쳐 두 번 반복되며,
- Stage 3: \( \frac{H}{16} \times \frac{W}{16} \times 4C\)
- Stage 4: \( \frac{H}{32} \times \frac{W}{32} \times 8C\)
이 단계들은 VGG나 ResNet과 같은 일반적인 CNN의 resolution과 동일한 feature map resolution으로 hierarchical representation을 만들어낸다. 결과적으로, 제안된 아키텍처는 다양한 비전 task를 위한 기존 방법의 backbone network를 효과적으로 대체할 수 있다.
4. Experiments (results)
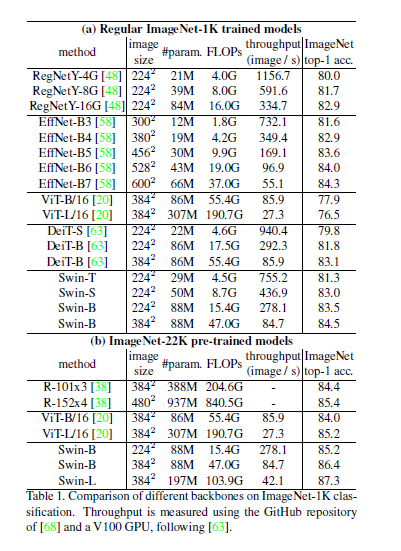
regular ImageNet-1K에 대해서 기존의 SOTA 트랜스포머 기반의 아키텍처와, SOTA CNN 모델들과 비교하여 더 나은 speed-accuracy tradeoff를 보여주고 있다(표의 (a)에 해당). 또한 ImageNet-22K로 pre-training한 뒤 ImageNet-1K로 fine-tuning한 Swin-B(base)와 Swin-L(large)의 성능도 타 모델과 비교해 뛰어난 성능을 보여주고 있음을 알 수 있다(표의 (b)에 해당).
자료 출처: https://greeksharifa.github.io/computer%20vision/2021/12/14/Swin-Transformer/



