[DL] 신경망의 개요 - Neural Networks와 역전파(Back propagation)

 

머신러닝 vs 딥러닝?

  본격적으로 신경망에 들어가기 앞서, 머신러닝과 딥러닝은 다른 것일까? 머신러닝이란 '기계가 경험을 통해 작업을 개선할 수 있도록 하는 기술'이다. 어쨋든 우리가 아는 ML/DL 알고리즘 모두 학습을 이용해 최적화하는 단계를 거치니까 딥러닝이 머신러닝의 부분집합임은 자명하다. 반면, 차이점으로 딥러닝은 인공신경망(ANN; Artificial Neural Network)을 기반으로 한다는 것에 있다. 그래서 딥러닝은 '연속된 층(layer)에서 점진적으로 의미 있는 표현을 배우는 기계 학습의 한 종류'라고 말할 수 있으며, 층 기반 표현 학습(layered representations learning) 또는 계층적 표현 학습(hierarchical representations learning)이라고 부르기도 한다. 따라서 딥러닝에 대해 배우고 싶으면 신경망이란 무엇인지, 층 기반 학습이란 무엇인지부터 알아야 한다.

 

 

출처 - https://docs.microsoft.com/ko-kr/azure/machine-learning/concept-deep-learning-vs-machine-learning

 

 

 

1. ANN (Artifical Neural Network)

  인공신경망이라고 불리는 ANN은 사람의 신경망 원리와 구조를 모방해 만든 머신러닝 알고리즘이다. 인간의 뇌는 수많은 뉴런(nueron; 신경세포)이 100조개 이상의 시냅스를 통해 병렬적으로 연결되어 있다. 이 시냅스는 뉴런과 뉴런을 연결하는 역할을 한다. 

 

(왼) 두뇌의 신경세포(뉴런) / (오) 인공신경망의 뉴런

 

인공신경망의 뉴런 모델은 생물학적인 뉴런을 수학적으로 모델링한 것이다. 두뇌의 뉴런이 입력값을 받아서 세포체에 저장하다가 자신의 용량을 넘어서면 외부로 출력값을 내보내는 것처럼, 인공신경망의 뉴런도 여러 입력값을 받아서 일정 수준이 넘어서면 활성화되어 출력값을 내보낸다(활성화 함수에 대한 설명은 이미 이 포스트에서 열심히 다뤘다).

 

 

ANN 기본 구조

 

• 입력층(Input layer): n개의 입력값들이 있다고 하면, 입력층은 n개의 노드를 가지게 됨
• 은닉층(Hidden layer): 모든 입력 노드들로부터 입력값을 받아 가중합을 계산하고, 이 값을 활성화 함수에 적용하여 출력층에 전달
• 출력층(Output layer): 출력값 산출 

 

순전파와 역전파

  우리는 손실함수와 경사하강법 포스트에서 이미 경사하강법이 무엇인지 배웠다. 예측값과 실제값 사이의 오차가 모든 데이터를 대상으로 최소가 되도록 신경망에서의 파라미터인 가중치(weight)와 편향(bias)를 결정함으로써 모델의 '최적화'를 수행한다. 그리고 이때의 손실함수(이를 포함해 신경망에 사용된 모든 연산이)가 미분 가능하다는 장점을 사용하여 네트워크 가중치에 대한 손실의 그래디언트(gradient)를 계산하는 것이 경사하강법이다.

 

기본적인 딥러닝 방식은 손실 점수(loss)를 피드백 신호로 사용해, 현재 샘플의 손실 점수가 감소되는 방향으로 가중치 값을 조금씩 수정하는 것이다 - training loop

 

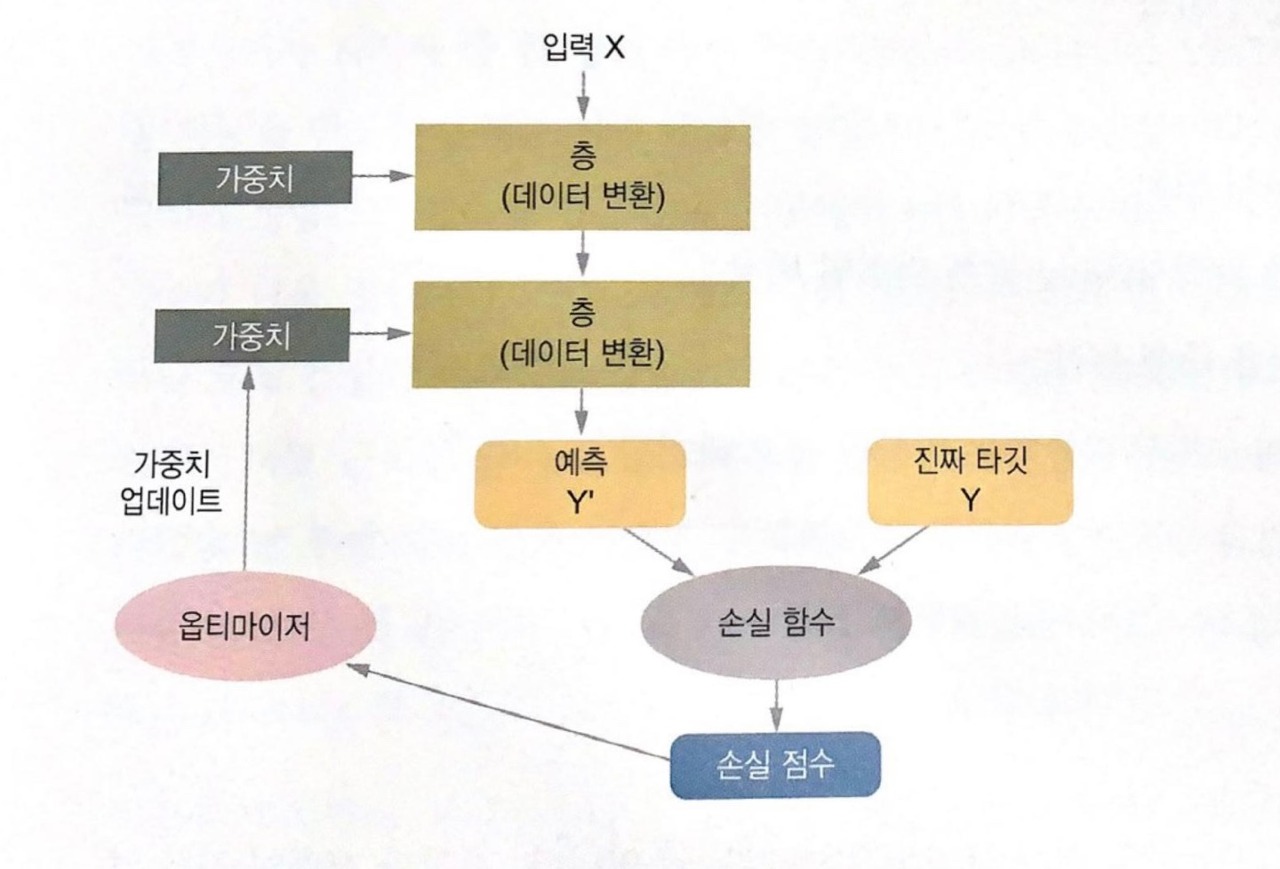
인공신경망은 경사하강법을 사용하여 순전파와 역전파 과정을 반복하면서 오차를 최소화하는 가중치를 찾는다. 순전파(forward propagation)은 말그대로 입력층->은닉층->출력층을 순서대로 거치면서 오차를 계산하는 과정이고, 역전파(back propagation)은 순전파와 반대로 츨력층->은닉층->입력층 순으로 가중치를 업데이트 해 나가는 과정이다. 역전파 과정에서 미분의 연쇄 법칙(chain rule)을 통해 가중치를 유도하게 된다(정확히는 편미분의 연쇄 법칙이다).

 

 

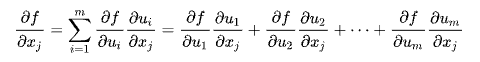
감이 안오는가? 예제를 통해 직접 손으로 계산해보자(길어서 접어놨다. 궁금하면 더보기 클릭). 참고로 해당 예제는 딥 러닝을 이용한 자연어 처리 입문 위키독스에서 가져왔다.

 

예제(2-2-2 다층 퍼셉트론)

• 2개의 입력층 뉴런, 2개의 은닉층 뉴런, 2개의 출력층 뉴런
• 활성화 함수= sigmoid \(f(z) = \frac{1}{1+e^{-z}} \)
• 학습률 \( \alpha \)는 임의의 수인 0.5로 설정
• 편향(bias) 생략

(1) 순전파

 

(2) 역전파 1단계 (출력층->은닉층)

 

 

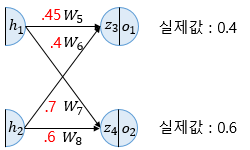
(3) 역전파 2단계 (은닉층->출력층)

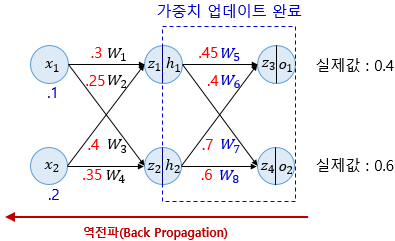
위에서 했던 것과 똑같은 방법으로 \( W1, W2, W3, W4 \)를 업데이트 해주면 됨 (힘들다 ^^...)

모든 가중치에 대한 업데이트가 끝났으면 다시 순전파 방향으로 \( o1, o2 \)를 계산해 실제값과 예측값의 오차제곱합을 구해 총 오차합 \( Etotal \)을 구해준다;

\( newE_{total} \)은 기존의 \( E_{total} \)보다 작음 → 다시 또 순전파와 역전파를 통해 가중치를 업데이트

이렇게 순전파와 역전파를 반복함으로써 오차를 최소화하는 가중치를 찾아간다!

 

 

 

2. DNN (Deep Neural Network)

  위에서 본 인공신경망으로도 이미 충분히 효과를 볼 수 있지만, 단점이 존재한다.

 

1. 학습과정에서 파라미터의 최적값을 찾기 어렵다.
   출력값을 결정하는 활성화함수의 사용은 기울기 값에 의해 weight가 결정되었는데 이런 gradient값이 뒤로 갈수록 점점 작아져 0에 수렴하는 오류를 낳기도 하고(gradient vanishing) 부분적인 에러를 최저 에러로 인식하여 더이상 학습을 하지 않는 경우도 있습니다.
2. Overfitting에 따른 문제
3. 학습시간이 너무 느리다.
   은닉층이 많으면 학습하는데에 정확도가 올라가지만 그만큼 연산량이 기하 급수적으로 늘어나게 됩니다.

 - 출처 : https://ebbnflow.tistory.com/119

 

그래서 등장한 것이 DNN이다. DNN은 ANN 내 은닉층을 늘려서 학습의 결과를 향상시킨 모델이다. 이런 DNN을 응용한 알고리즘으로 합성곱신경망(CNN), 순환신경망(RNN), 그리고 순환신경망 계열 LSTM, GRU 등이 있다.