저번 포스트에서는 sound 데이터를 어떻게 딥러닝에서 이용할 수 있는 디지털 데이터로 변환할 수 있는지에 대해 이론적으로 알아보았다. 이번 포스트에서는 python의 librosa 라이브러리로 직접 데이터를 전처리, 가공하는 과정을 기록해보려고 한다.
librosa는 음악과 오디오 분석을 위한 파이썬 패키지로, 신호 처리에 필요한 계산식을 numpy 기반으로 처리해준다. 자세한 설명 및 튜토리얼은 librosa 공식 도큐멘테이션 참고.
librosa — librosa 0.9.2 documentation
© Copyright 2013--2022, librosa development team.
librosa.org
** prerequisite - 개발환경에 librosa가 설치되어 있어야 한다.
# install through Python Package Index(PyPI)
pip install librosa
# install on conda environment
conda install -c conda-forge librosa
1. Audio loading
이번 실습에 사용할 sound 데이터를 불러온다. 베토벤의 가장 유명한 교향곡 제5번의 첫 20초 가량을 담은 wav파일을 사용해보았다.
import os
import numpy as np
import matplotlib.pyplot as plt
import librosa, librosa.display
# load audio file with librosa package
file = "Beethoven_5th_Symphony.wav"
signal, sample_rate = librosa.load(file)
# draw a waveform
FIG_SIZE = (12, 5)
plt.figure(figsize=FIG_SIZE)
librosa.display.waveshow(signal, sample_rate, alpha=0.5)
plt.xlabel("Time (s)")
plt.ylabel("Amplitude")
plt.title("Original waveform")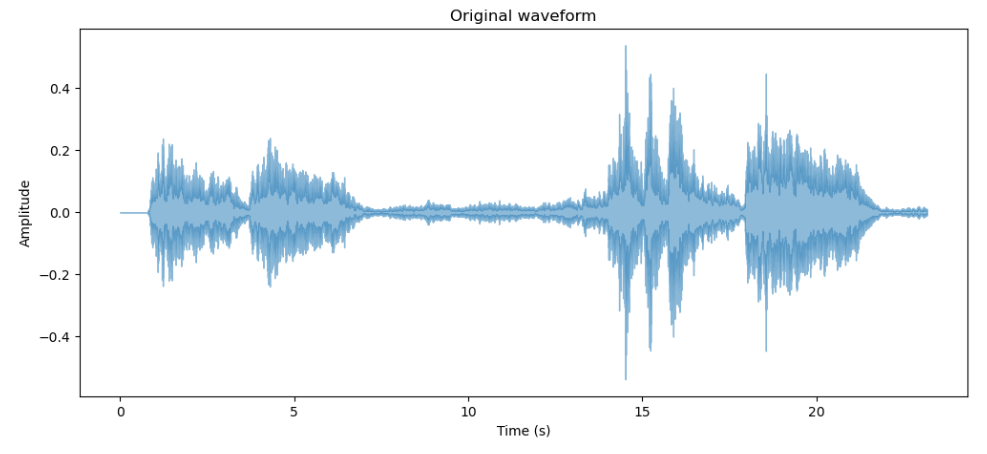
librosa.load 함수는 오디오 파일을 부동 소수점 단위의 time series 데이터로 출력한다. 중요한 것은 이 함수에 sr이라는 파라미터가 존재하는데, 위의 예시처럼 명시해주지 않을 시 native sample rate인 22050으로 다시 샘플링된다. 기억해두지 않으면 추후 모델 학습할 때 삐꾸가 날 수 있기 때문에(경험담^^;;), 파일의 기존 sample rate을 보존하고 싶다면 파라미터로 꼭 명시해두길..
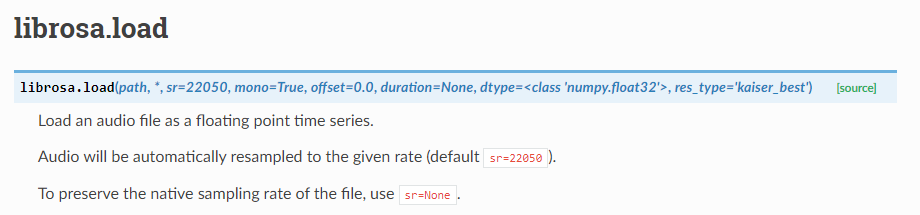
2. Extracting spectral features
2-1. Spectrogram
audio feature의 첫 번째 단계라고 볼 수 있는 스펙트로그램부터 계산해보자. 한 두줄이면 STFT 바로 계산 가능 ^^
복습 - x축이 시간, y축이 주파수가 되도록 STFT 데이터를 그래프로 나타낸 것을 스펙트로그램이라고 한다.
FRAME_SIZE = 2048
HOP_SIZE = 512
S_scale = librosa.stft(signal, n_fft=FRAME_SIZE, hop_length=HOP_SIZE)
S_scale
여기서 갑자기 왜 abs(절댓값)을 계산해주지? 이유는 librosa.stft의 결과가 복소수라는 것에 있다 - 위 그림의 STFT 결과값이 array, dtype=complex64 -. 이 복소수는 오디오 시그널의 주기(phase)와 진폭(amplitude) 값을 나타내는데, 주기는 인간이 인식할 수 없기 때문에 사실상 진폭에 대한 정보만 필요하며 이는 복소수의 절댓값으로 구할 수 있다. (피타고라스의 정리에 기반한 복소수의 절댓값을 구하는 기하학적 해석에 대해서는 Wikipedia에 잘 정리되어있음)
따라서 librosa.stft에 절댓값을 계산해 실수 단위로 변환, power spectrogram scale로 맞춰주는 코드를 추가로 작성하면 스펙트로그램 그래프를 볼 수 있다.
# calculate STFT
S_scale = librosa.stft(signal, n_fft=FRAME_SIZE, hop_length=HOP_SIZE)
Y_scale = np.abs(S_scale) ** 2
# draw a spectrogram
plt.figure(figsize=FIG_SIZE)
img = librosa.display.specshow(Y_scale, sr=sample_rate, hop_length=HOP_SIZE, x_axis="time", y_axis="linear")
plt.title("Spectrogram")
plt.colorbar(format="%+2.f")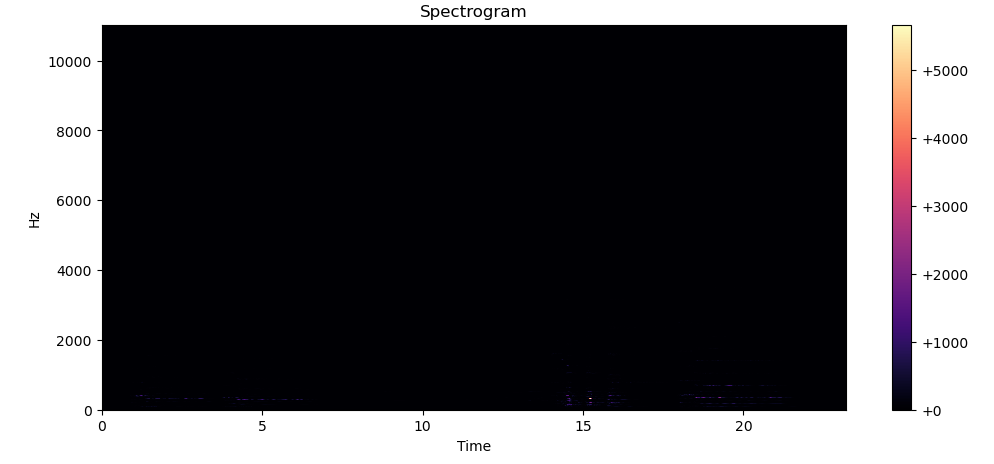
??? 컬러 차트의 색깔이 밝으면 밝을 수록 energy intensity가 높다는 뜻인데, 아무것도 안보인다!
쓸모있는 스펙트로그램을 뽑으려면 scaling이 필요하다. 저번 포스트에서 소리의 높낮이와 세기는 logarithmically 인식된다고 설명한 바 있다.
revisit -
Mel-scale과 Decibel-scale: 인간은 소리의 요소 중 하나인 주파수를 선형 척도가 아닌 로그 척도(log scale)로 인식하며 소리의 또 다른 요소인 진폭 또한 logarithmically 인식된다.
이 두 요소를 로그 스케일로 조정해준다. 이러면 이제 잘보이지!
# log-amplitude spectrogram
Y_log_scale = librosa.power_to_db(Y_scale)
# ㅣog-frequency spectrogram
plt.figure(figsize=FIG_SIZE)
img = librosa.display.specshow(Y_log_scale, sr=sample_rate, hop_length=HOP_SIZE, x_axis="time", y_axis="log")
plt.title("Log-scaled spectrogram (amplitude/frequency)")
plt.colorbar(format="%+2.f dB")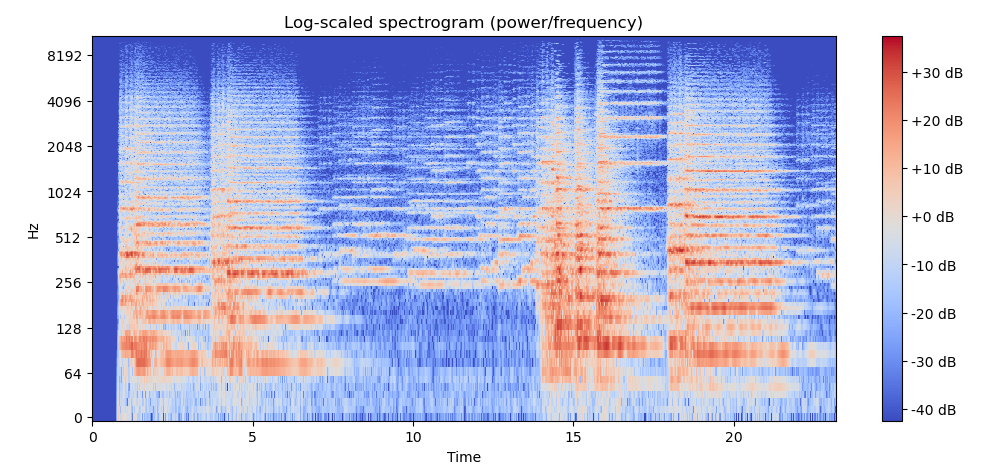
여기서 얻을 수 있는 교훈은 결국 스펙트로그램 그 자체는 오디오 데이터 분석에 있어 별 도움이 안되는 representation이라는 것이다. 단순히 로그 스케일로 변환하는 것 말고 다른 효과적인 방식들도 아래에 소개한다.
2-2. Mel-spectrogram
로그 변환과 밀접하게 맞닿아 있는 것이 mel-scale transformation이다. librosa.feature.melspectrogram을 통해 original signal → STFT → mel-scale transformation → decibel-scale transformation 후 완성된 mel-spectrogram을 얻을 수 있다.
wav 파일 로드부터 시작하는 full code는 다음과 같다.
import os
import numpy as np
import matplotlib.pyplot as plt
import librosa, librosa.display
# load wav file
FIG_SIZE = (12, 5)
file = "Beethoven_5th_Symphony.wav"
signal, sample_rate = librosa.load(file)
# compute through pre-computed power spectrogram
FRAME_SIZE = 2048
HOP_SIZE = 512
Y_scale = np.abs(librosa.stft(signal, n_fft=FRAME_SIZE, hop_length=HOP_SIZE)) ** 2
M_scale = librosa.feature.melspectrogram(S=Y_scale, sr=sample_rate)
M_log_scale = librosa.power_to_db(M_scale, ref=np.max)
# draw a Mel-spectrogram
plt.figure(figsize=FIG_SIZE)
img = librosa.display.specshow(M_log_scale, sr=sample_rate, x_axis="time", y_axis="mel")
plt.title("Mel-spectrogram")
plt.colorbar(format="%+2.f dB")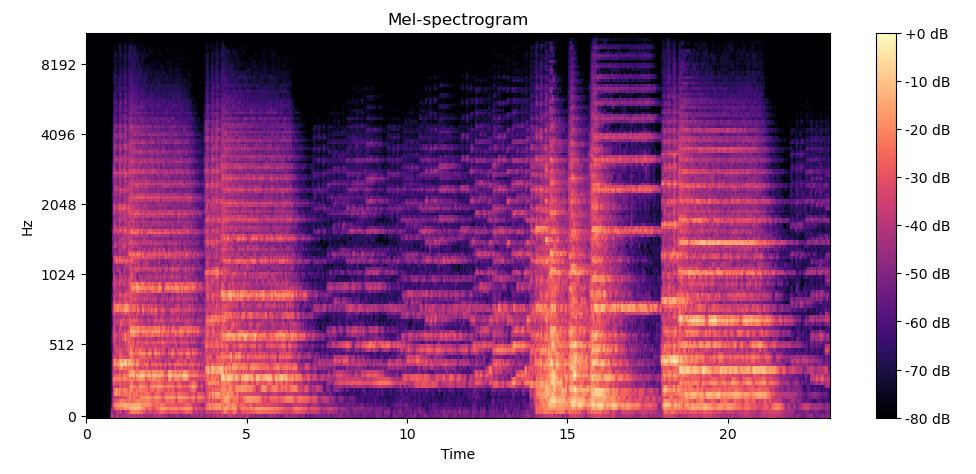

mel-spectrogram은 다음과 같은 하이퍼 파라미터들이 존재하는데, 주요하게 tuning해 볼 만한 것은 n_fft와 hop_length 정도가 있다.
STFT는 이미 설명했지만, 원본 신호를 frame 단위로 짧게 잘라 각 frame에 DFT를 수행한 것이다. 이때 이 frame의 길이가 n_fft이다. 일반적으로 이러한 frame들은 정보의 손실을 피하기 위해 일정 구간 겹쳐진다.
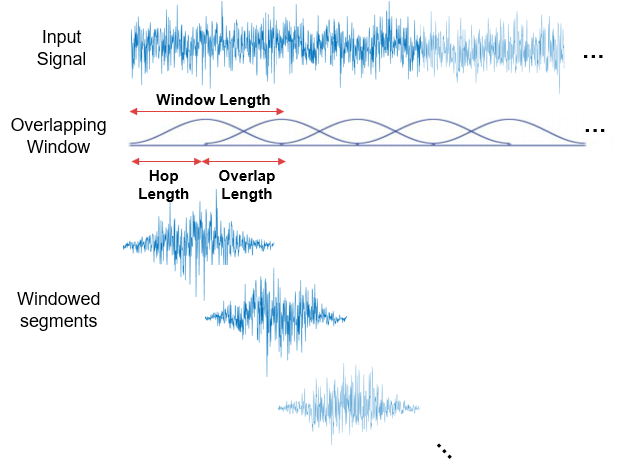
따라서 두 frame 사이의 거리는 종종 n_fft가 아니라 n_fft/2와 같이 계산되는데, 이것이 hop_length이다. 가령 1000개의 오디오 샘플이 있고 hop_length가 100이라면, 10개의 feature frame이 도출된다. 추가로 참고할 만한 사항은, n_fft가 hop_length보다 크다면 padding이 필요한데 이 때 window_length라는 파라미터를 조정해주면 된다.
2-3. MFCC
MFCC는 스펙토그램보다는 스펙트럼과 더 밀접한 관련이 있기 때문에 위 방식과는 전혀 다르게 계산되어야 한다(spectrum <-> cepstrum). librosa 공식 도큐멘테이션을 따라 실습해본 full code는 다음과 같다.
# load wav file
FIG_SIZE = (12, 10)
file = "Beethoven_5th_Symphony.wav"
signal, sample_rate = librosa.load(file)
# compute mel-spectrogram and MFCC with y, sr
FRAME_SIZE = 2048
HOP_SIZE = 512
M_scale = librosa.feature.melspectrogram(y=signal, sr=sample_rate)
M_log_scale = librosa.power_to_db(M_scale, ref=np.max)
mfcc = librosa.feature.mfcc(S=M_log_scale, sr=sample_rate)
# draw two plot of audio features
fig, ax = plt.subplots(nrows=2, figsize=FIG_SIZE, sharex=True)
img_ms = librosa.display.specshow(M_log_scale, x_axis='time', y_axis='mel', ax=ax[0])
fig.colorbar(img_ms, ax=[ax[0]])
ax[0].set(title='Mel-spectrogram')
ax[0].label_outer()
img_mf = librosa.display.specshow(mfcc, x_axis='time', ax=ax[1])
fig.colorbar(img_mf, ax=[ax[1]])
ax[1].set(title='MFCC')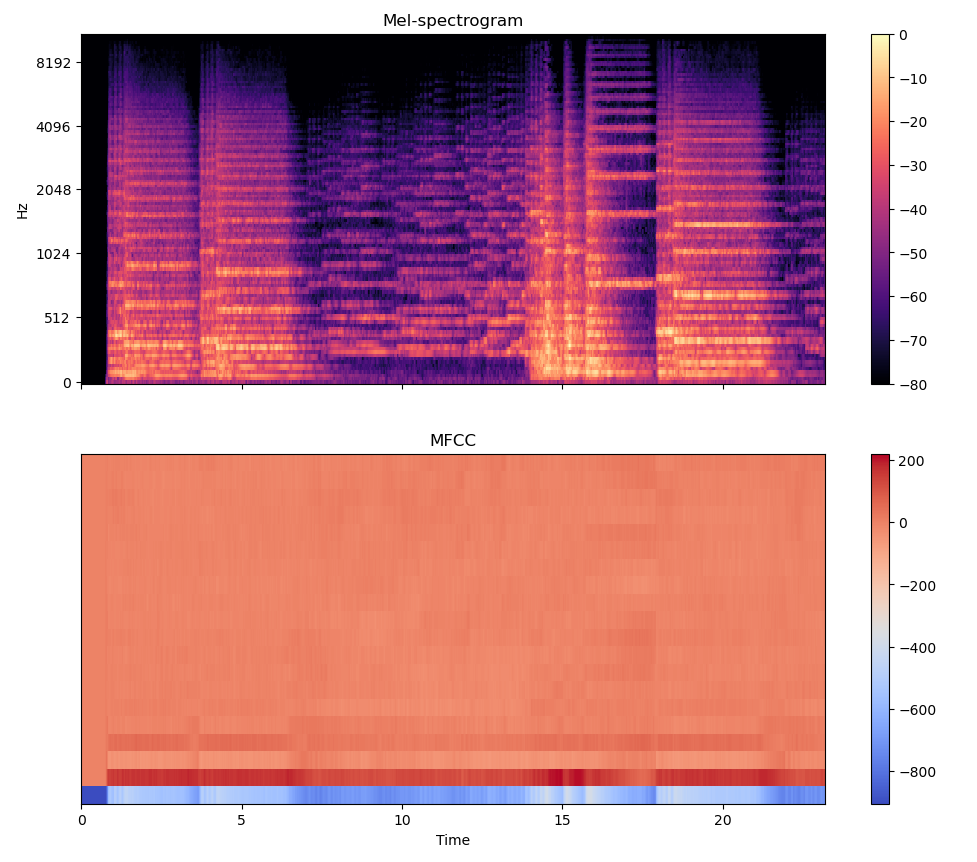
3. Other forms
기존 포스트에서 CQT를 언급했던 기억이 있어, CQT 변환을 통한 스펙트럼 산출물도 소개해보려한다.
# load wav file
FIG_SIZE = (12, 5)
file = "Beethoven_5th_Symphony.wav"
signal, sample_rate = librosa.load(file)
# compute CQT
CQT_scale = np.abs(librosa.cqt(y=signal, sr=sample_rate))
CQT_log_scale = librosa.amplitude_to_db(CQT_scale, ref=np.max)
# draw a CQT spectrum
plt.figure(figsize=FIG_SIZE)
img = librosa.display.specshow(CQT_log_scale, sr=sample_rate, x_axis="time", y_axis="cqt_note")
plt.title("Constant-Q power spectrum")
plt.colorbar(format="%+2.f dB")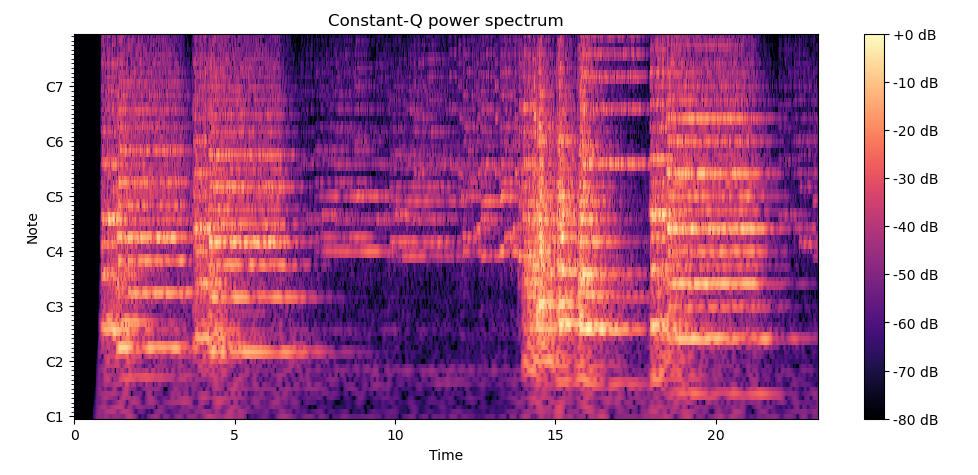
'AI > Deep Learning' 카테고리의 다른 글
| [DL] CUDA, cuDNN이란? - layered architecture for Deep Learning (0) | 2022.12.30 |
|---|---|
| [DL] 딥러닝 음성 이해 - Introduction to sound data analysis (1) | 2022.12.02 |
| [DL] keyword extraction with KeyBERT - 개요 및 알고리즘 (0) | 2022.03.28 |
| [DL] Topic modeling with BERTopic - 개요 및 알고리즘 (0) | 2022.03.27 |
| [DL] Exploding & Vanishing Gradient 문제와 Residual Connection (0) | 2022.03.17 |



