AVL트리에 대해 알아보자.
이전 포스트에서, BST 순회와 연산의 시간복잡도를 줄이기 위해 균형잡힌 이진트리를 만든다고 했었다. 그 중 한 방법이 AVL트리이다. AVL트리는 모든 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차가 1이하이다. 그리고 노드가 삽입되는 과정에서 스스로 노드들을 재배치해서 균형 상태를 유지한다.
균형 인수 = 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
'AVL트리이다'는 말은 모든 노드의 균형 인수가 다음을 충족시킬 때를 일컫는다.
-1 <= balance factor(균형인수) <= 1
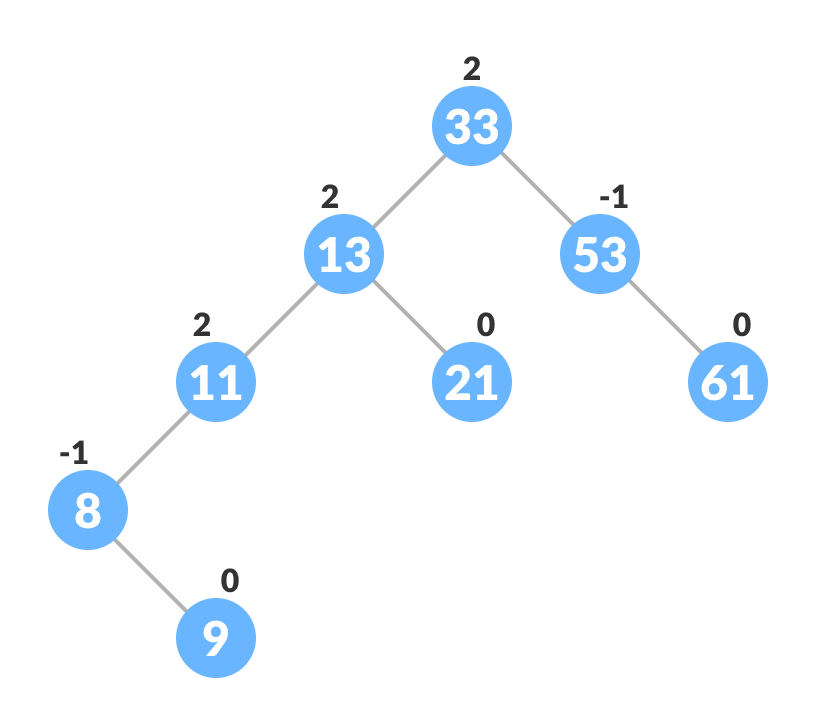
평균, 최선, 최악의 경우의 시간복잡도는 전부 O(log(n))이다. BST에서 최선의 경우 시간복잡도가 O(log(n)), 최악의 경우 O(n)이었던걸 떠올려보면 확실히 효율성이 높다.
BST에서는 삭제연산이 까다로웠다. AVL트리에서는 삽입연산이 관건이다...
AVL트리의 삽입연산
노드 N을 삽입할 때, 노드 N으로부터 가장 가까우면서 균형인수가 2가 된 조상 노드가 A라면
(1) AVL트리의 균형이 깨지는 4가지의 경우
- LL타입: N이 A의 왼쪽 서브트리의 왼쪽 서브트리에 삽입
- LR타입: N이 A의 왼쪽 서브트리의 오른쪽 서브트리에 삽입
- RR타입: N이 A의 오른쪽 서브트리의 오른쪽 서브트리에 삽입
- RL타입: N이 A의 오른쪽 서브트리의 왼쪽 서브트리에 삽입
(2) 각 타입별 재균형 방법
- LL회전: A부터 N까지의 경로상 노드의 오른쪽 회전
- LR회전: A부터 N까지의 경로상 노드의 왼쪽-오른쪽 회전 (RR회전->LL회전)
- RR회전: A부터 N까지의 경로상 노드의 왼쪽 회전
- RL회전: A부터 N까지의 경로상 노드의 오른쪽-왼쪽 회전 (LL회전->RR회전)
그림으로 보자.
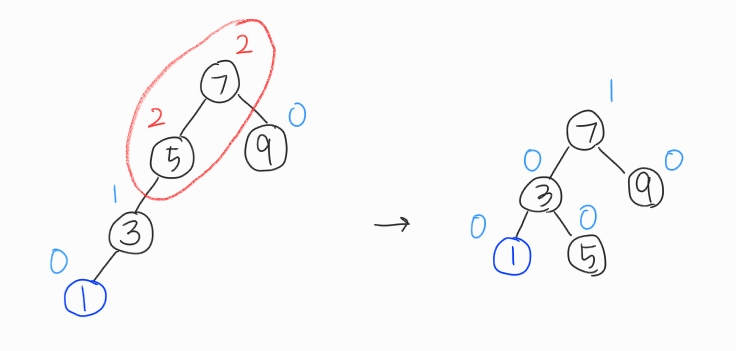
노드 1을 삽입했다. 3보다 작기 때문에 3의 왼쪽자식으로 배정. 하지만 노드 5와 7의 균형인수가 2를 넘어버렸다! 이럴때는 노드 1과 가장 가까우면서 균형이 깨진 조상노드를 찾아야 하는데, 노드 5이다. 노드 5를 기준으로 LL회전(5부터 1까지의 경로상 노드의 오른쪽 회전)을 해주면 된다. 이름이 LL회전인데 오른쪽으로 돌려야 한다ㅋㅋ..
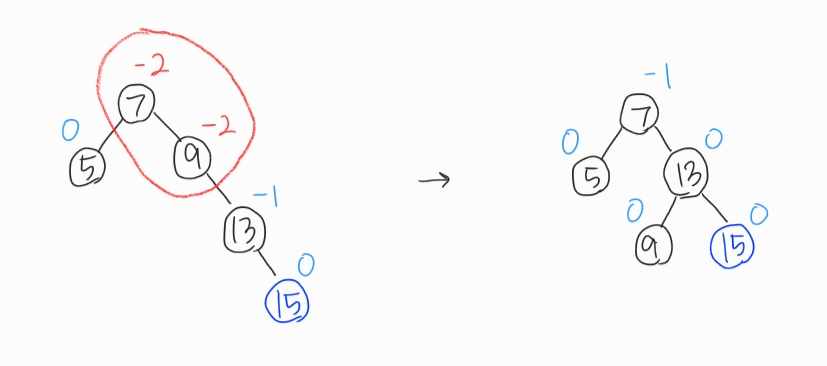
LR회전과 RL회전을 하려면 RR회전을 먼저 알아야되기 때문에 RR회전부터 설명하겠다. 이번엔 노드 15를 삽입해보았다. 노드 7과 9의 균형이 깨졌고, 노드 15로부터 가장 가까운 조상노드는 9이기 때문에 9를 기준으로 RR회전(9부터 15까지의 경로상 노드의 왼쪽 회전). 참고로 15는 9의 오른쪽 서브트리의 오른쪽 서브트리에 삽입된 것이기 때문에 RR타입이라고 판단할 수 있다. 이것도 RR회전인데 왼쪽으로 돌리네... 이름을 왜 이렇게 지은거야
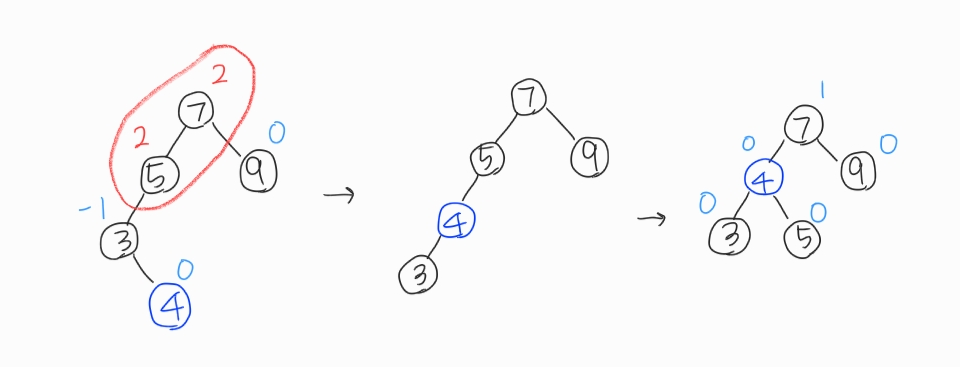
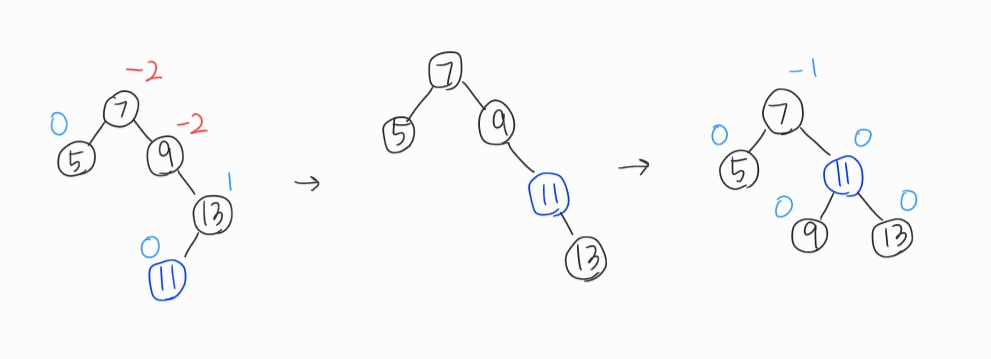
LR회전과 RL회전은 LL회전과 RR회전을 한 번씩 다 해줘야 해서 총 3단계이다.
LR회전: RR회전->LL회전, 즉 왼쪽으로 돌렸다가 오른쪽으로 돌리기
RL회전: LL회전->RR회전, 즉 오른쪽으로 돌렸다가 왼쪽으로 돌리기
이다.
중요한 건 두 회전 중 처음 하는 회전은 균형이 깨진 인자를 포함해서 돌리면 안된다!! 가령 위에 LR회전을 보면, 처음에 RR회전을 시킬 때 노드 5를 포함하지 않는다. 마지막에 LL회전 할 때만 노드 5 포함해서 총 3개의 노드를 돌림.
{7, 8, 9, 2, 1, 5, 3, 6, 4}의 노드들을 입력한 순서대로 삽입해보자
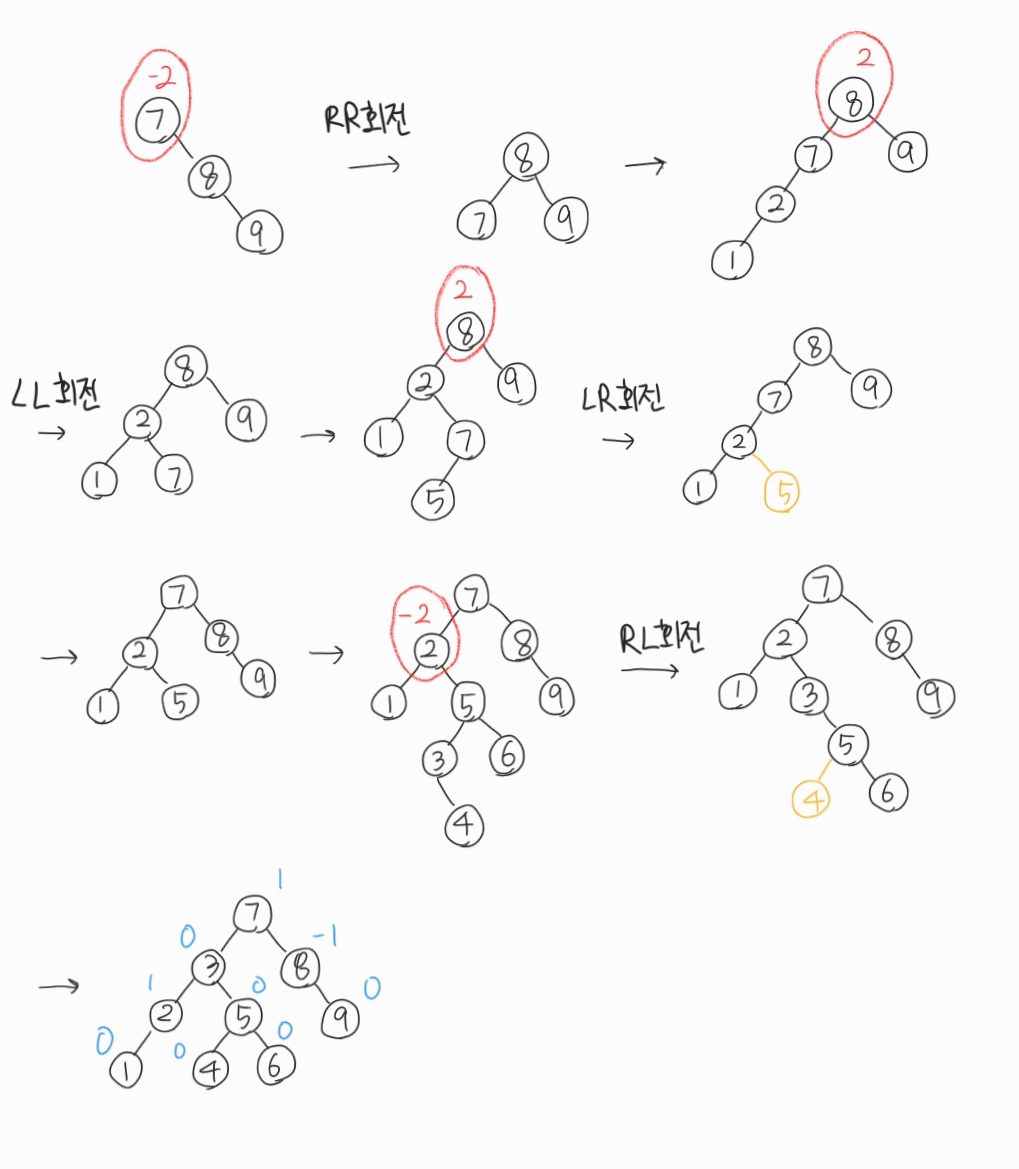
의문이 있다. 노란색으로 표시된 부분인데, 삽입된 노드를 기준노드의 자식에게 물려줘야 하나??! 왜 그런 설명은 들은 적이 없는 것 같지??
'coding > Data Structure(C)' 카테고리의 다른 글
| [C] 그래프와 DFS, BFS 구현 (0) | 2020.12.14 |
|---|---|
| [C] 힙과 우선순위 큐 (0) | 2020.12.13 |
| [C] 이진탐색트리(BST; Binary Search Tree) (0) | 2020.12.13 |
| [C] 이진트리의 순회 (0) | 2020.12.12 |
| [C] 트리와 이진트리 (0) | 2020.12.12 |



