[강화학습] CH02-1. 마르코프 결정 프로세스(MDP; Markov Decision Process)

 

  저번 챕터에서 강화학습이 해결하고자 하는 순차적인 의사결정 문제란 무엇인지 간략하게 살펴보았다. 순차적인 의사결정 문제는 마르코프 결정 프로세스(MDP)라는 개념을 통해 수식으로 더 명확하게 이해할 수 있다. 이를 위해 마르코프 프로세스부터 차례차례 알아보자.

 

 

1. 마르코프 프로세스 (Markov Process)

MP modeling

 

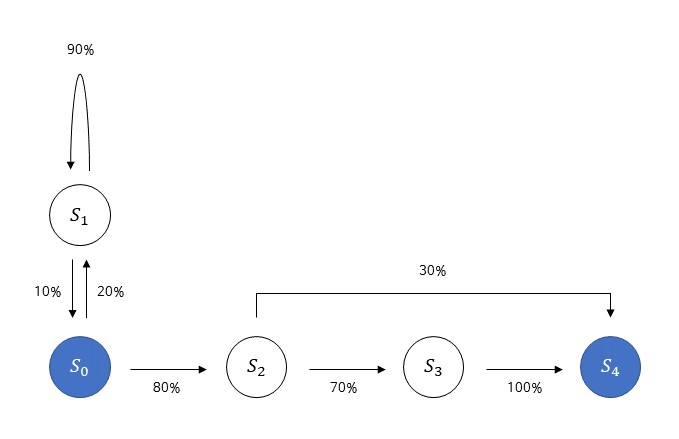
  \( s_0 \)부터 시작하는 5가지 상태 \( {s_0, s_1, s_2, s_3, s_4} \)가 있다고 가정해보자. \( s_0\)에서 시작하는 여정은 다음 상태로 넘어가는 상태 전이(state transition)을 통해 진행된다. \( s_4 \)는 종료 상태(terminal state)로, 이곳에 도달하는 순간 마르코프 프로세스는 끝난다. 여기서 마르코프 프로세스란 미리 정의된 어떤 확률 분포를 따라서 상태와 상태 사이를 이동해 다니는 여정이다. 가령 위 그림에서 \(s_2\)에서 \(s_3\)로 이동할 확률은 70%이다. 나머지 30%의 확률은 \(s_4\)로 바로 이동하는 것으로, 하나의 상태에서 다른 상태로 이동하는 화살표의 합은 항상 100%이다.

$$ MP \equiv (S, P) $$

• 상태 집합 \( S \) : \(S = \{s_0, s_1, .., s_4 \} \)
• 전이 확률 행렬 \( P_{ss'} \) : \( P_{ss'} = P[S_{t+1}=s' | S_t = s] \)

  상태의 집합 \(S \)는 가능한 상태들을 모두 모아놓은 집합이고, 전이 확률 행렬(transition probability state) \(P_{ss'}\)는 상태 \(s \)에서 다음 상태 \( s' \)에 도착할 확률이다. 가령 위의 그림에서 \(s_0\)에서 시작해 \(s_1\)에 도착할 확률 \( P_{s_0s_1}\)은 20%이다.

 

 

마르코프 성질 (Markov property)

  마르코프 프로세스(이하 MP)의 모든 상태는 마르코프 성질을 따른다. 즉, 

$$ P[s_{t+1} | s_t] = P[s_{t+1} | s_0, s_1, ..., s_t] $$

위의 식은 "미래는 오로지 현재에 의해 결정된다"고 해석할 수 있다. 상태가 \( s_{t+1} \)이 될 확률을 계산하려면, 그 전에 어떤 상태들이 오든 상태 \(s_t \)가 무엇인지만 주어지면 충분하다는 것이다. 

A Markov process is a stochastic process that satisfies the Markov property(sometimes characterized as "memorylessness"). In simpler terms, it is a process for which predictions can be made regarding future outcomes based solely on its present state and—most importantly—such predictions are just as good as the ones that could be made knowing the process's full history. In other words, conditional on the present state of the system, its future and past states are independent.

 - 출처 : https://en.wikipedia.org/wiki/Markov_property

 

  어떤 현상을 MP로 모델링 하려면 상태가 마르코프 해야 한다. 

 

 

 

2. 마르코프 리워드 프로세스 (Markov Reward Process)

  MP에 보상의 개념이 추가되면 마르코프 리워드 프로세스(이하 MRP)가 된다.

MRP modeling

 

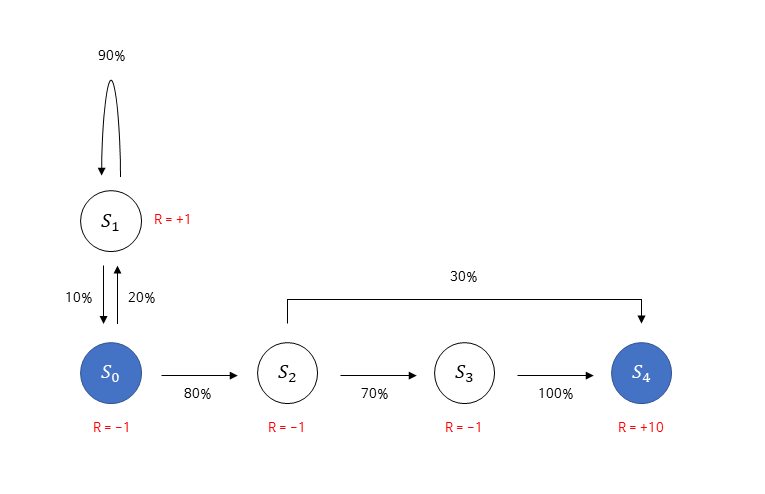
  그림에 추가된 빨간색 값은 보상(reward)으로, 이제 어떤 상태에 다다르게 되면 보상을 받게 된다. 이전 포스트에서 우리는 강화학습이란 누적 보상을 최대화하는 방향으로 학습하는 방법론이라는 것을 배웠으므로, 보상이라는 요소가 추가적으로 필요함을 알 수 있다.

 

$$ MRP \equiv (S, P, R, \gamma) $$

• 보상 함수 \(R \) : \( R = E[R_t | S_t = s] \)
• 감쇠 인자 \( \gamma \) : 0~1 사이의 양수

  보상 함수 \(R\)은 어떤 상태 \(s\)에 도달했을 때 받게되는 보상을 말한다. 식에서 기댓값이 등장한 이유는 특정 상태에 도달했을 때 받는 보상이 매번 조금씩 다를 수도 있기 때문에 보편성을 더해주기 위한 것이다. 보상 함수뿐만 아니라 감쇠 인자 \( \gamma \)도 MRP에 추가되는데, 감쇠 인자란 강화 학습에서 미래에 얻을 보상에 비해 당장 얻는 보상을 얼마나 더 중요하게 여길 것인지를 나타내는 파라미터이다. 감쇠 인자는 1보다 작은 양수이기 때문에 미래에 얻을 보상의 값에 여러 번 곱해지며 그 값을 작게 만든다.

 

 

리턴 (Return)

  감쇠 인자를 정확하게 이해하기 위해서는 리턴(return)이란 무엇인지 알아야한다. 리턴은 \(t\) 시점부터 미래에 받을 감쇠된 보상의 합을 말한다(중요한 것은 "누적" 보상이란 것을 잊지 말자. 다시 말해, 강화 학습은 보상을 최대화하는 것이 아니라 리턴을 최대화하는 것이다!!).

  강화 학습에서 에피소드(episode)란 시작 상태부터 종료 상태까지 에이전트가 거친 상태나 행동, 보상의 sequence를 의미한다. 그림에서 \( s_0\)부터 시작하여 \(s_4\)까지 가는 여정을 표기하면 다음과 같다.

$$ s_0, R_0, s_1, R_1, ..., s_4, R_4 $$

이런 에피소드 표기법을 통해 리턴 \( G_t \)를 정의할 수 있다.

$$ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... $$

 

위 식에서 타임스텝 \(t \)가 커질수록 \( \gamma \)가 여러 번 곱해지는 것을 볼 수 있다. \( \gamma \)의 크기를 통해 미래에 얻게 될 보상에 비해 현재에 얻는 보상에 가중치를 주는 것이다. 그렇다면 미래의 보상은 왜 현재 보상에 비해 가중치가 낮을까?

 

1. 수학적 편리성 - \( \gamma \)를 1보다 작게 해줌으로써 리턴 \( G_t \)가 무한의 값을 가지는 것을 방지
2. 사람의 선호 반영 - 사람은 기본적으로 당장 벌어지는 눈앞의 보상을 더 선호
3. 미래에 대한 불확실성 반영 - 현재와 미래 사이에는 다양한 확률적 요소들이 있어 미래에 어떤 일이 벌어질지 모름

 

 

3. 마르코프 결정 프로세스 (Markov Decision Process)

 

출처 -https://blog.paperspace.com/reinforcement-learning-for-machine-learning-folks/

 

  지금까지 살펴본 MP와 MRP에서는 에이전트가 딱히 하는 일이 없었다. 이말인 즉슨, 상태 변화가 자동으로 이루어지고 있었으며 다음 상태의 분포 또한 이미 정해져 있었다. 순차적 "의사결정"이랄 것이 없었는데, 마르코프 결정 프로세스(이하 MDP)에 들어와서는 의사를 가지고 행동하는 주체인 에이전트와 에이전트의 행동인 액션(action)이 등장한다.

 

$$ MDP \equiv (S, A, P, R, \gamma) $$

• 액션의 집합 \( A\) : 상태 \(s\)에서 취할 수 있는 액션들을 모아놓은 finite set
• 전이 확률 행렬 \( P_{ss'}^a \) : \( P_{ss'}^a = P[S_{t+1} = s' | S_t = s, A_t = a] \)
• 보상 함수 \(R_s^a \) : \( R_s^a = E[R_{t+1} | S_t = s, A_t = a] \)

  에이전트가 취하는 액션을 \(a \)라 한다면, 이를 모아놓은 집합 \( A \)가 등장하고 전이 확률 행렬과 보상 함수에 \(a\)와 관련된 조건들이 추가된다. MDP의 \( P_{ss'}^a \)는 현재 상태가 \(s\)이며 에이전트가 액션 \(a\)를 선택했을 때, 다음 상태가 \(s' \)이 될 확률을 말한다(MP, MRP에서 \( P_{ss'} \)는 현재 상태가 \(s\)일 때 다음 상태가 \(s' \)이 될 확률을 뜻했다). 또, 보상함수 \(R_s^a \)는 상태 \(s\)에서 액션 \(a\)를 선택하면 받는 보상을 가리킨다. MRP에서 어떤 상태 \(s\)에 도달하면 받는 보상 \(R\)과 액션이 있고 없고의 관점에서 다르다. MDP에서는 액션이 추가 되어 현재 상태 \(s \)에서 어떤 액션을 선택하느냐에 따라 보상이 달라지기 때문이다.