이번 포스트에서는 RNN부터 시작해 순환 신경망 계열 딥러닝 모델들의 구조를 살펴보도록 하겠다. 즉, RNN, LSTM, 그리고 GRU에 대한 내용이 될 것이다.
앞서 살펴봤던 기본 ANN과 합성곱 신경망 CNN, 그리고 완전 연결 네트워크(fully-connected layer을 사용한)의 특징은 메모리가 없다는 것이다. 네트워크에 주입되는 입력은 개별적으로 처리되며 입력 간에 유지되는 상태가 없다는 것이다. 반면 오늘 정리할 순환 신경망 계열 모델들은, 이전에 나온 정보를 기억하면서 다음 데이터들을 학습할 수 있다는 특징 때문에 텍스트와 시퀀스 데이터를 처리할 때 자주 사용된다.

1. 순환 신경망 (RNN; Recurrent Neural Network)
RNN은 시계열 데이터와 같이 시간의 흐름에 따라 변화하는 데이터를 학습하기 위해 등장한 인공신경망이다. RNN은 생물학적 지능처럼, 정보 처리를 위해 내부 모델을 유지하면서 점진적으로 정보를 처리한다.

위와 같은 문장을 학습하려고 한다고 해보자. 전체가 한 문장이다(...) 특별한 처리를 해주지 않는 한 컴퓨터는 사람이 문장을 읽을 때처럼 맥락을 이해할 수 없을 것이다. 그리고 점점 뒤로 갈수록 앞의 정보들이 소실되는 현상이 일어난다. 이를 해결하기 위해 순환 신경망 계열 모델에서는 시퀀스의 원소를 순회하면서 지금까지 처리한 정보를 상태(state)에 저장한다.
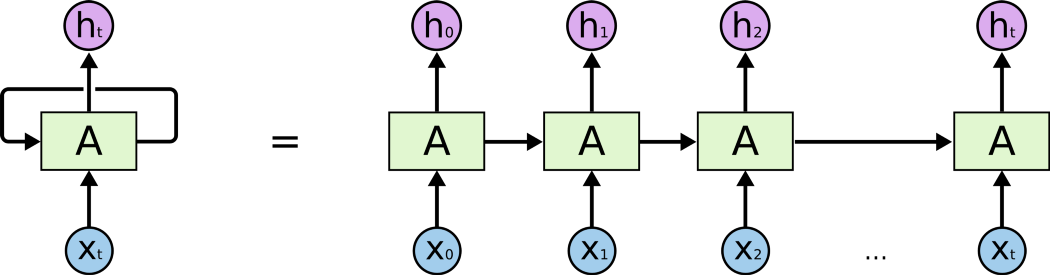
- A는 뉴럴넷 덩어리, \( X_t \)는 입력값, \( h_t \)는 결과값
순환 신경망의 구조는 재귀함수와 같은 형태를 취하고 있다. 이를 우변에서처럼 펼쳐보면, 현재의 state가 그 다음 state에 영향을 미치고 있는 것을 알 수 있다. 은닉층의 노드에서 활성화 함수를 통해 나온 결과값을 출력층 방향으로도 보내면서, 다시 은닉층 노드의 다음 계산의 입력으로 보내는 것이 순환 신경망 계열 모델들의 공통적인 특징이다.
기본 구조
간단히 말하면 RNN은 내부에 루프를 가진 신경망의 한 종류이다.

현재 시점 t에서의 은닉 상태값을 \( h_t \)라고 한다면, \( h_t \)를 계산하기 위해서는 총 두개의 가중치 \( W_x \)와 \( W_h \)를 알아야 한다. \( W_x \)는 입력층에서 입력값을 위한 가중치이고, \( W_h \)는 이전 시점인 t-1의 은닉 상태값인 \( h_{t-1} \)을 위한 가중치값이다. 즉, 현재 은닉 상태값 \( h_t \)와 출력값 \( y_t \)는 다음과 같이 나타낼 수 있다.
- 은닉층 \( h_t = tanh(W_xx_t + W_hh_{t-1} + b) \)
- 출력층 \( y_t=f(W_yh_t+b) \)
내부 학습 과정
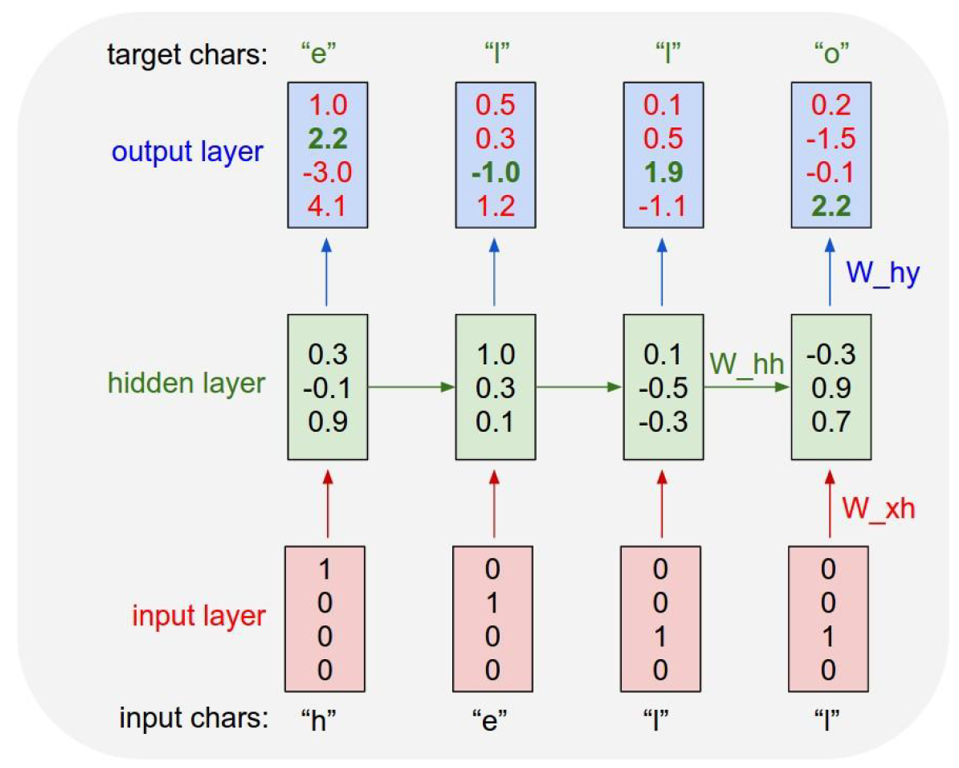
RNN이 "hello"라는 단어를 학습한다고 해보자. 첫번째 은닉층 \( h_1 \)의 값은 random하게 설정된다(\( h_0 \)는 존재하지 않기 때문에). 이를 바탕으로 \( y_1 \)인 [1.0, 2.2, -3.0, 4.1] 벡터를 생성한다. 마찬가지로 각각의 입력값 \( x_2, x_3, ... \)에 대해서도 은닉층 \( h \)을 거쳐 출력값을 생성한다. 이 과정이 순전파(forward propagation)이다. 순전파와 역전파에 대한 자세한 설명 및 계산식은 이전 포스트를 참조.
RNN은 지도 학습이며, 다음에 올 글자를 맞추기 위해 순서의 패턴을 학습해야 한다. 출력층의 output \( y \)을 보면 초록색으로 강조된 부분이 있을 것이다(\( y_1 \)의 경우 2.2이다). 이는 'h' 다음 글자인 'e'를 맞추기 위해 정답을 주는 것이다. 이를 바탕으로 역전파(back propagation)을 수행하며 가중치를 갱신해나간다. 따라서 RNN이 학습하는 파라미터(가중치)로는 입력값을 은닉층 \(h\)로 보내는 \( W_{xh} \), 이전 은닉층에서의 \( W_{hh} \), 은닉층 \( h \)에서 출력층 \( y \)로 보내는 \( W_{hy} \)이다.
2. 장단기 메모리 (LSTM; Long Short-Term Memory)
장기 의존성 문제 (the problem of Long-Term Dependencies)
바닐라 RNN의 대표적인 단점은 비교적 짧은 시퀀스에 대해서만 효과를 보인다는 것이다. 바닐라 RNN은 실전에서 쓰기에는 너무 단순하다. 이론적으로 시간 t에서 이전의 모든 타임스텝의 정보를 유지할 수 있지만, 실제로는 긴 시간에 걸친 의존성은 학습할 수 없다는 것이 문제이다. 이는 층이 많은 일반 네트워크에서 나타나는 그래디언트 소실 문제(vanishing gradient problem)와 비슷하다. 시점 t가 길어질수록 앞의 정보가 뒤로 충분히 전달되지 못하는 현상이 발생하므로, 이를 해결하기 위해 LSTM과 GRU가 고안되었다.
기본 구조
LSTM은 앞서 보았던 RNN의 한 변종이다. SimpleRNN에 정보를 여러 타임스텝에 걸쳐 나르는 방법이 추가된다. LSTM 셀의 역할은 과거 정보를 나중에 주입하여 의존성 문제를 해결하는 것이다.
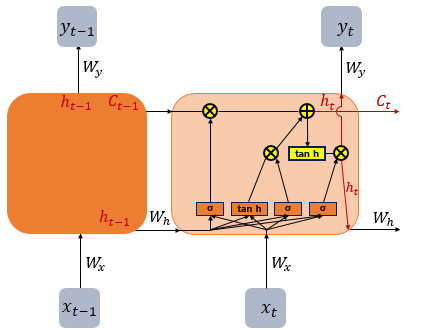
복잡하다ㅎㅎ... cell state \( C_t \)는 타임스텝 t를 가로질러 정보를 나르는 데이터의 흐름이다. 이 \( C_t \)가 추가된 LSTM에서 데이터가 학습되는 과정을 살펴보자.
내부 components
LSTM은 은닉층의 메모리 셀에 입력 게이트(input gate), 망각 게이트(forget gate), 출력 게이트(output gate)를 추가하여 불필요한 기억을 지우고 기억해야 할 것들을 정한다.
(1) 망각 게이트 (Forget Gate)
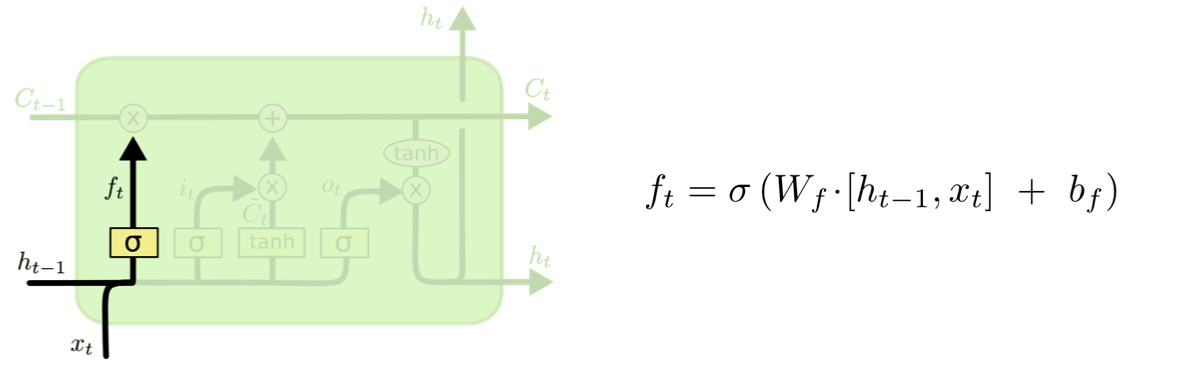
Decide what information we’re going to throw away from the cell state
시그모이드 함수를 사용해, 출력값이
- '0'일 경우, 이전의 cell state값은 모두 0이 되어 미래의 결과에 아무런 영향을 주지 못하게 된다.
- '1'일 경우, 미래의 예측 결과에 영향을 주도록 이전의 cell state \( C_{t-1} \)을 그대로 보내 완전히 유지한다.
(2) 입력 게이트 (Input Gate)
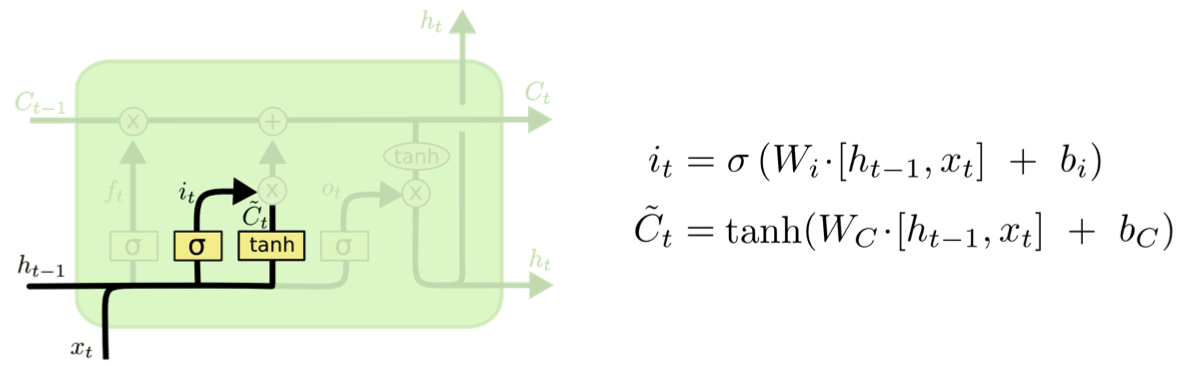
현재 정보를 기억하기 위한 게이트이다.
- \( i_t \): 시그모이드 함수를 지나므로 0과 1 사이의 값
- \( \tilde{C_t} \): tanh 함수를 지나므로 -1과 1 사이의 값
(3) 셀 상태 (Cell State)
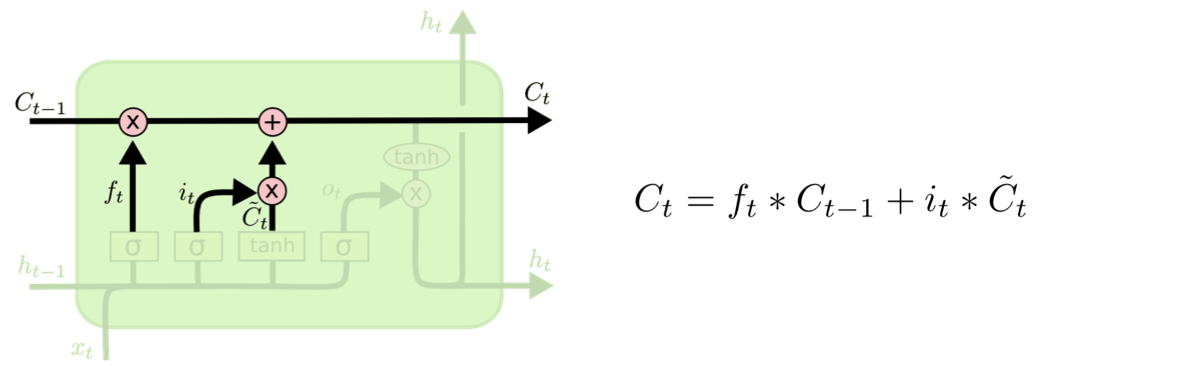
타임스텝 t에서의 이동 상태 \( C_t \)로, 망각 게이트를 지나오면서 일부 기억을 잃은 상태이다(\( f_t * C_{t-1} \)의 식에서 알 수 있음, 이는 이동을 위한 데이터 흐름에서 관련이 적은 정보를 의도적으로 삭제하는 것이라고 볼 수 있다).
- 입력 게이트에서 구한 \( i_t, \tilde{C_t} \)에 대해서 원소별 곱(entrywise product) 수행
- 입력 게이트에서 선택된 기억을 망각 게이트의 결과값과 더함 - 현재 시점 t의 cell state
- \( t+1 \) 시점의 LSTM 셀로 넘겨짐
(4) 출력 게이트 (Output Gate)
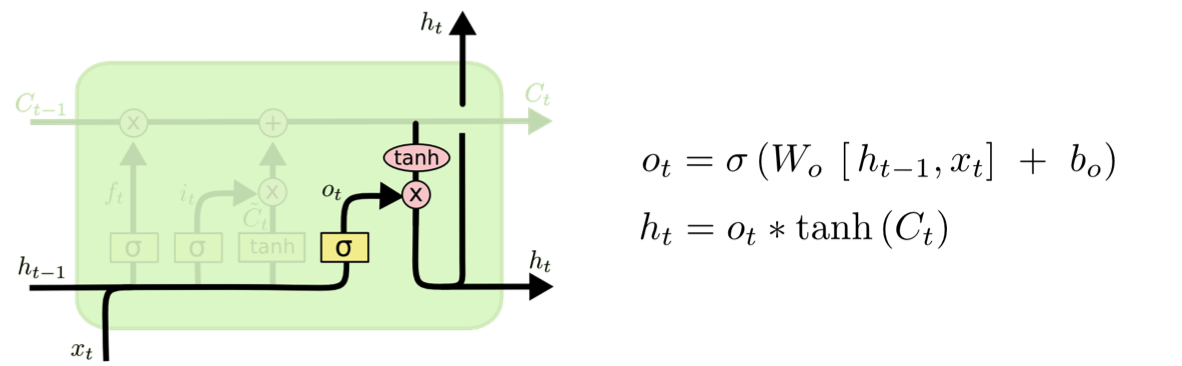
Output based on the updated state
최종적으로 얻어진 cell state 값을 얼마나 빼낼지 결정하는 역할을 한다.
3. 게이트 순환 유닛 (GRU; Gate Recurrent Unit)
GRU는 2014년에 조경현 박사님 등이 개발하였다(그래서 같이 공부하던 오빠들이 K-RNN이라 불렀던ㅋㅋㅋㅋ웃김). LSTM과 같은 원리로 작동하지만 조금 더 간결하고, 그래서 계산 비용이 덜 든다. 대신 계산 비용과 표현 학습 능력 사이의 trade-off는 ML 어디에서나 존재하므로 LSTM만큼 표현 학습 능력이 높지는 않을 수도 있다. GRU가 타 순환 신경망 계열 모델보다 항상 더 좋은 성능을 발휘하지는 않는다는 뜻이다.
기본 구조
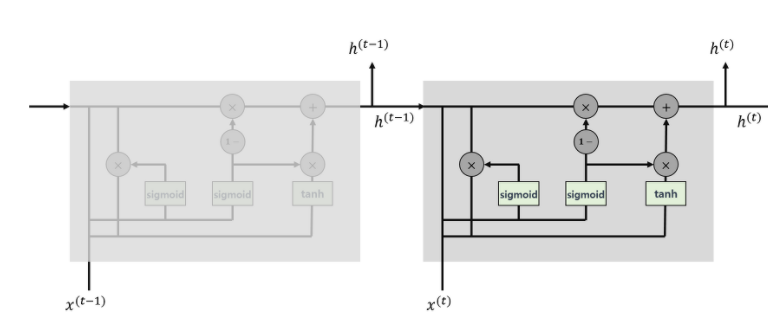
GRU 셀에는 리셋 게이트와 업데이트 게이트, 이렇게 두 가지 게이트만이 존재한다. LSTM을 간단화한 구조를 갖고 있기 때문이다.
내부 components
(1) 리셋 게이트 (Reset Gate)
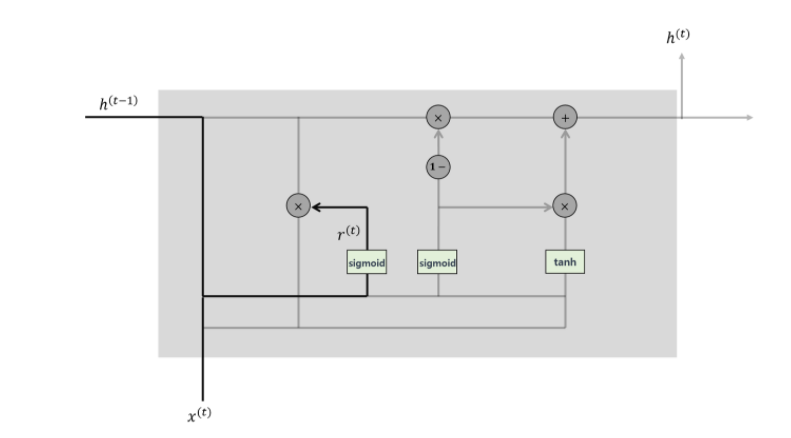
과거의 정보를 적당히 리셋시킨다. 이전 은닉층을 지나 도출되는 가중치 \( r^{(t)} \)의 식은 다음과 같다.
$$ r^{(t)}=\sigma(W_{r}h^{(t-1)}+U_{r}x^{(t)}) $$
(2) 업데이트 게이트 (Update Gate)
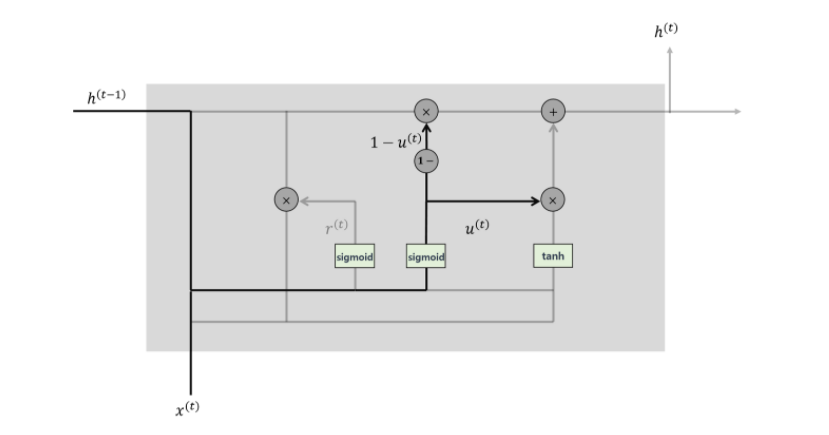
LSTM의 망각 게이트와 입력 게이트의 역할을 합쳐놓은 것과 같다고 보면 된다. 과거와 현재의 정보의 최신화 비율을 결정한다.
\( u^{(t)} \)를 현 시점 정보의 양이라고 하면
$$ u^{(t)}=\sigma\left(W_{u}h^{(t-1)}+U_{u}x^{(t)}\right) $$
\( u^{(t)} \)를 계산한 후 \( 1- u^{(t)} \)를 직전 시점의 은닉층의 정보에 곱해준다.
(3) Candidate
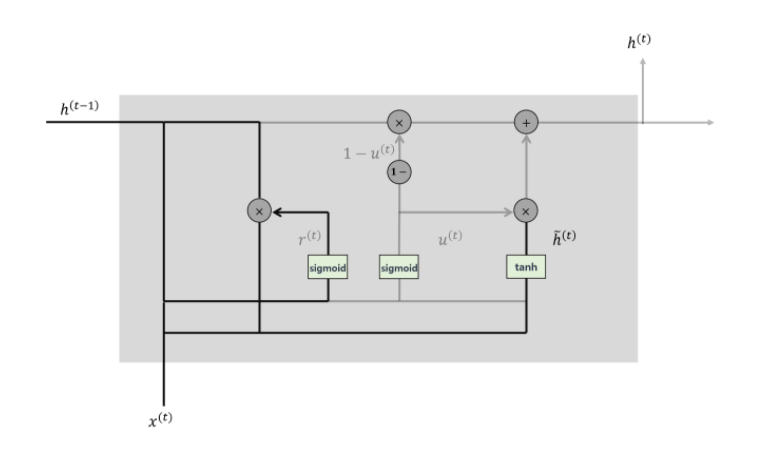
리셋 게이트의 결과를 곱하여 현 시점 t의 정보 후보군을 결정하는 단계이다.
$$ \tilde{h^{(t)}}=\tau\left(Wh^{(t-1)}*r^{(t)}+Ux^{(t)}\right) $$
(4) 은닉층 계산
업데이트 게이트와 candidate의 결과를 결합하여 현 시점의 은닉층 가중치를 계산한다.
$$ h^{(t)}=(1-u^{(t)})*h^{(t-1)}+u^{(t)}*\tilde{h}^{(t)} $$
'AI > Deep Learning' 카테고리의 다른 글
| [DL] 텍스트 데이터와 언어 모델(Language Model) (0) | 2022.03.10 |
|---|---|
| [DL] Attention 파헤치기 - Seq2Seq부터 Transformer까지 (2) (0) | 2022.03.08 |
| [DL] Attention 파헤치기 - Seq2Seq부터 Transformer까지 (1) (0) | 2021.11.10 |
| [DL] 합성곱 신경망(CNN; Convolutional Neural Network) 파헤치기 (0) | 2021.10.18 |
| [DL] 신경망의 개요 - Neural Networks와 역전파(Back propagation) (0) | 2021.10.18 |



