[ML] 활성화 함수(Activation Function) 종류 정리
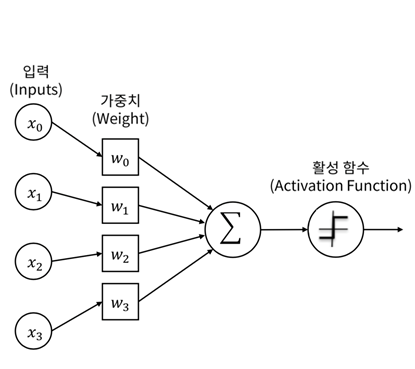
신경망에서는 노드에 들어오는 값들에 대해 곧바로 다음 레이어로 전달하지 않고 활성화 함수를 통과시킨 후 전달한다. 활성화 함수(activation function)는 입력 신호의 총합을 출력 신호로 변환하는 함수로, 입력 받은 신호를 얼마나 출력할지 결정하고 네트워크에 층을 쌓아 비선형성을 표현할 수 있도록 해준다.
활성화 함수는 주로 비선형이다. 왜 비선형인가? 선형함수를 사용할 시 층을 깊게 하는 의미가 줄어들기 때문이다.
예를 들어 16개의 은닉 유닛을 가진 2개의 완전 연결층과, 스칼라 값의 예측을 출력하는 세 번째 층을 쌓아보자.
from keras import models
from kears import layers
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(1000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
여기서 활성화 함수인 relu를 제외한다면, output의 계산식은 다음과 같아진다.
output = dot(W, input) + b
즉, 가중치와 편향만으로 이루어진 선형 연산이 된다. 이는 가설공간에 제약이 생긴다는 얘기인데, 선형 층을 깊게 쌓아도 여전히 하나의 선형 연산이기 때문에 층을 여러개로 쌓는 이점이 사라진다. 신경망에서 층을 쌓는 혜택을 얻고 싶다면 활성화 함수로는 반드시 비선형 함수를 사용해야 한다.

1. 시그모이드 함수 (Sigmoid function)
활성화 함수의 대표적인 예로, 정의는 다음과 같다.
$$ \sigma(x) = \frac{1}{1+e^{-x}}, e=2.718281... $$
이거 어디서 많이 봤다. 이 포스트에서 다뤘던 로지스틱 회귀함수와 모양이 비슷하다. 로지스틱 회귀모형은 독립변수가 \( [-\infty, \infty] \)의 어느 숫자이든 상관없이 종속변수(결과값)이 항상 범위 [0,1] 사이에 있도록 한다. 이때 사용되는게 활성화 함수가 시그모이드 함수이다.
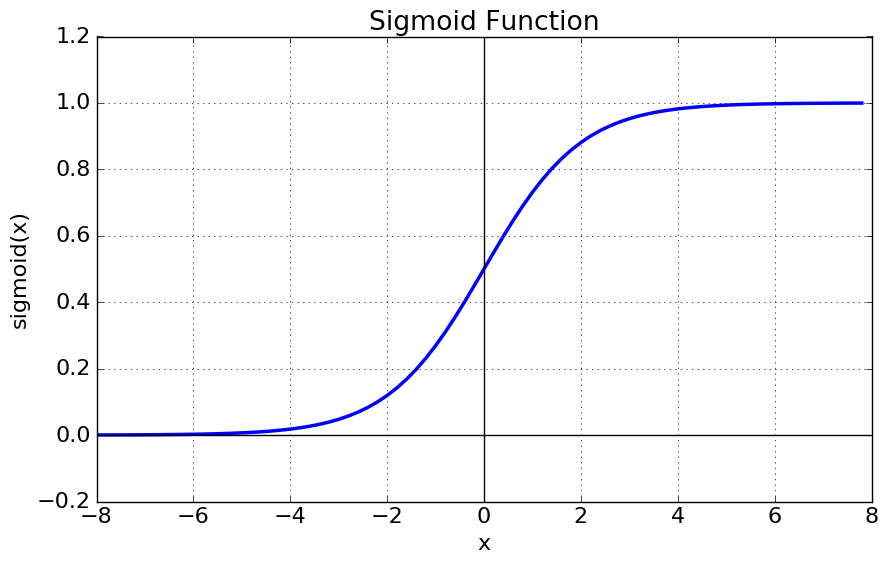
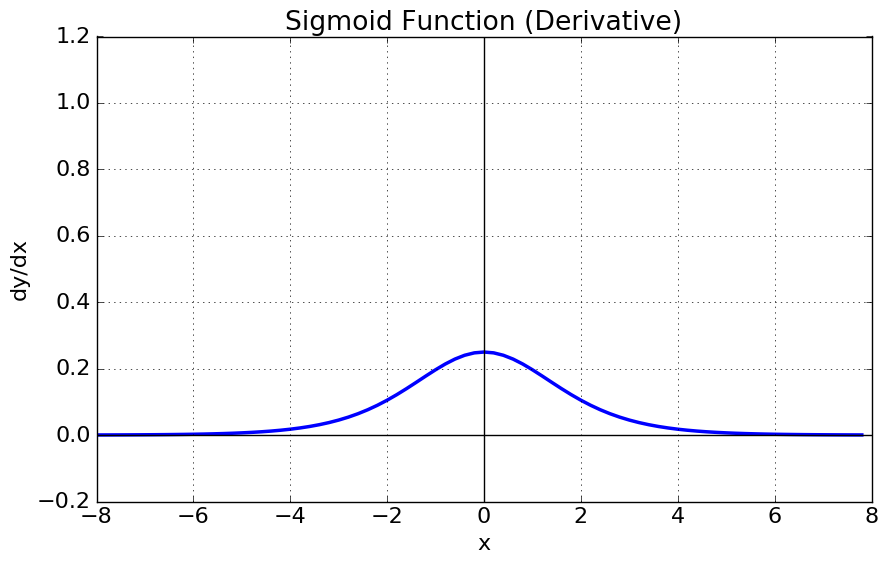
시그모이드 함수 \( \sigma(x) \)의 출력은 0보다 크고 1보다 작은 임의의 값이다. 또한 미분 가능 함수이다. 따라서 이진분류(binary classification) 문제에서 자주 사용하지만, 이 0과 1로 강제 출력하는 부분에서는 학습이 잘 이루어지지 않는다. 이를 기울기 소실(vanishing gradient) 문제라고 한다.
- Vanishing Gradient: 시그모이드의 미분함수(오른쪽 그림)를 보면 \( x=0 \)에서 최대값 1/4를 가지고, input값이 일정 이상 올라가면 미분한 값이 거의 0에 수렴하게 된다. 이는 역전파되는 과정에서 출력값이 현저하게 감소되는 결과를 낳는다(0에 가까운 값끼리 곱하면 0에 계속 가까워지듯이).
또, 시그모이드 함수는 zero-centered 하지 않아 학습이 느려질 수 있다. 이게 무슨 뜻이냐...

Zero-centered란 그래프의 중심 0인 형태로 함숫값이 양수 혹은 음수에만 치우치지 않고 실수 전체에서 나타나는 형태를 의미한다. Sigmoid는 위의 그래프에서도 볼 수 있듯이 함숫값이 항상 0보다 크거나 같은 형태로 나타난다. Neural networks에서 input은 이전 layer의 결과값이라고 생각하면 된다. 그런데 sigmoid 함수는 항상 양수이기에 sigmoid를 한번 거친 이후론 input 값은 항상 양수가 된다. 그렇게 되면 backpropagation을 할 때 문제가 생긴다. Backpropagation을 할 때 \( \frac{∂L}{∂w}=\frac{∂L}{∂a} \frac{∂a}{∂w} \) 그리고 \( \frac{∂a}{∂w}=x \)이기 때문에 \( \frac{∂L}{∂w}=\frac{∂L}{∂a}x \)이다. 그런데 input 값인 x는 항상 양수이기에 \( \frac{∂L}{∂w} \)와 \( \frac{∂L}{∂a} \)의 부호는 같을 수 밖에 없다. 2차원 평면에서 살펴보면 부호가 모두 같은 지점은 1,3 사분면 뿐이다. 따라서 지그재그의 형태로 학습이 될 수 밖에 없고 이는 학습을 오래 걸리게 한다.
- 출처 : https://velog.io/@ryuni/CS231n-Lec6
2. Tanh (Hyperbolic Tangent function)
시그모이드 함수를 변형한 쌍곡선 함수이다.
$$ tanh(x)=\frac{e^x−e^{−x}}{e^x+e^{−x}} $$
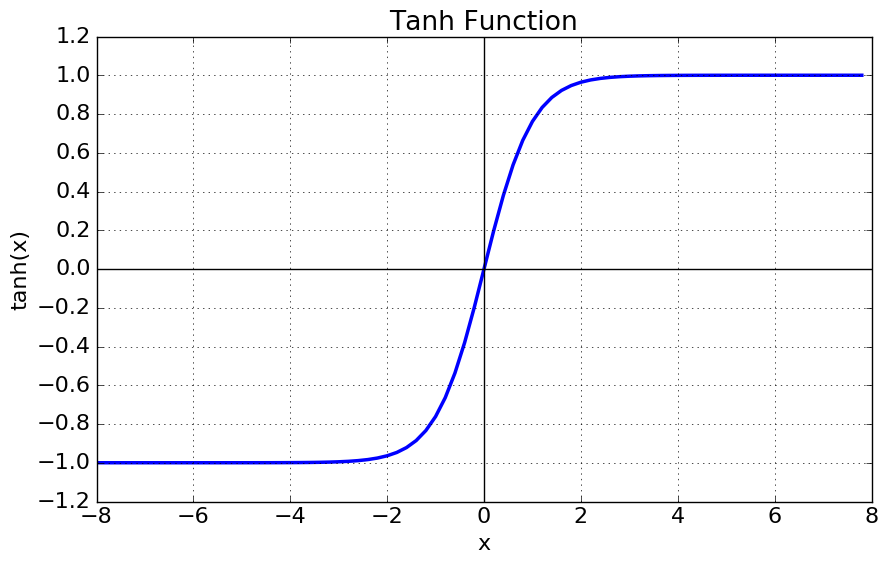

tanh 그래프의 미분함수를 보면 최댓값이 1이다. 시그모이드 미분함수와 비교하면 최댓값이 4배가 크다(위에서 시그모이드 미분함수의 최댓값은 1/4임을 밝혔다). 또, 시그모이드 함수의 단점인 non zero-centered를 해결했다. 하지만 여전히 vanishing gradient 문제는 해결하지 못했다. 그리고 이건 활성화 함수들의 고질적인 문제이다.
3. 소프트맥스 함수 (Softmax function)
소프트맥스 함수는 input값을 [0,1] 사이의 값으로 모두 정규화하여 출력하며, 출력값들의 총합은 항상 1이 되는 특성을 가진 함수이다. 다중분류(multi-class classification) 문제에서 사용한다. 분류될 클래스가 n개라고 할 때, n차원의 벡터를 입력받아 각 클래스에 속할 확률을 추정한다. 확률값을 반환한다는 점에서 시그모이드와 비슷하지만, 시그모이드 함수를 통과해 얻은 확률값들은 서로 독립적이다. 가령 3개의 클래스가 있다고 하면, 데이터 포인트가 클래스 1에 속할 확률은 다른 두 클래스의 확률을 고려하지 않는다. 따라서 multi-class classification에서 시그모이드 함수는 사용할 수 없고, 대신 소프트맥스 함수를 사용한다.
정의는 다음과 같다.
$$ softmax(x_i) = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}} $$
- n = 출력층의 뉴런 수 (총 클래스 수)
- x = x번째 클래스
예를 들어, 총 클래스 수가 3개라고 한다면 다음과 같은 결과가 나온다.
$$ softmax(x) = \left [ \frac{e^{x_1}}{e^{x_1}+e^{x_2}+e^{x_3}}, \frac{e^{x_2}}{e^{x_1}+e^{x_2}+e^{x_3}}, \frac{e^{x_3}}{e^{x_1}+e^{x_2}+e^{x_3}} \right ] = [p_1, p_2, p_3] $$
이것도 어디서 많이 봤다. 각각 [x번일 확률 / 전체확률]이다. 맞다, 값들이 확률분포를 이룬다.
소프트맥스 함수 그래프는... 정확히 나와있는게 없다. 소프트맥스는 일반적으로 다변수 함수이기 때문에(변수 3개 이상) 각각의 확률분포를 2차원으로 매핑하기 어렵다 3차원이면 몰라도..
4. Relu 함수 (Rectified Linear Unit function)
아마 제일 많이 사용되는 활성화 함수일 것이다. 거의 모든 CNN 네트워크나 딥러닝에 사용된다. 식은 다음과 같다.
$$ f(x)=max(0,x) $$

장점(1) - Sparsity : 뉴런의 활성화값이 0인 경우, 어차피 다음 레이어로 연결되는 가중치를 곱하더라도 결과값은 0을 나타내게 되서 계산할 필요가 없기에 sparse한 형태가 dense한 형태보다 더 연산량을 월등히 줄여준다. 단, x<0 인 값들에 대해서는 기울기가 0이기 때문에 뉴런이 죽을 수 있는 단점이 존재함.
장점(2) - Vanishing Gradient 해결(어느정도만...): ReLU의 역함수는 1이므로 ReLU의 경우에는 gradient로 상수를 갖게됨 → 일정한 gradient값은 빠르게 학습하는 것을 도와준다.
ReLU는 많이 사용되기 때문에 이를 기반으로 한 변형도 많다.
- Leakly ReLU - ReLU의 뉴런이 죽는(“Dying ReLu”)현상을 해결하기위해 나온 함수
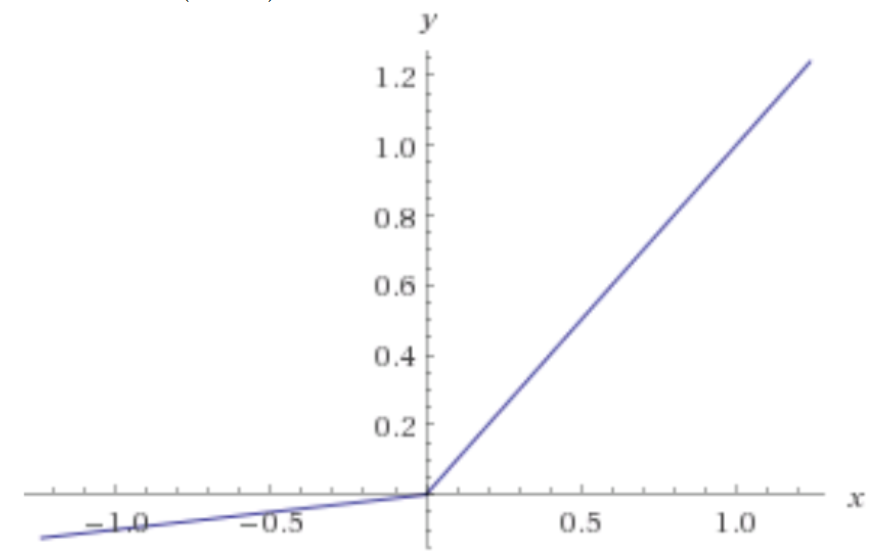
$$ f(x)=max(0.01x,x) $$
* 위 식에서 0.01 대신 다른 매우 작은 값 사용 가능
- PReLU - 새로운 파라미터 α 를 추가하여 x<0에서 기울기를 학습할 수 있게 함
(Leaky ReLU랑 다른게 뭐임?;;)

$$ f(x)=max(αx,x) $$
- Exponential Linear Unit(ELU) - 비용을 0으로 더 빨리 수렴하고 보다 정확한 결과를 도출함. 다른 활성화 함수와는 달리 ELU에는 양수여야 하는 \( \alpha \) 상수가 있다. 마이너스 값의 입력을 제외하고 ReLU와 매우 유사함.

x>0 일 때 \( f(x)=x \)
x≤0 일 때 \( f(x)=α(ex−1) \)