[ML] 토픽 모델링(Topic Modeling)

AI/Machine Learning

[ML] 토픽 모델링(Topic Modeling) - LSA와 LDA

heeee__ya 2022. 3. 13. 19:06

Topic modeling is a method for unsupervised classification of such documents, similar to clustering on numeric data, which finds natural groups of items even when we're not sure what we're looking for.

토픽 모델링(topic modeling)은 문서 집합(코퍼스) 안에서의 추상적인 "주제"를 찾기 위한 비지도학습 분류 방법이다. 사람은 글을 읽으며 자연스럽게 문서의 중심 아이디어를 찾아낸다. 마찬가지로 토픽 모델링은 머신러닝 및 자연어 처리 분야에서 컴퓨터가 텍스트 본문의 숨겨진 의미 구조를 발견하기 위해 사용되는 텍스트 마이닝 기법이라고 할 수 있다.

1. LSA (Latent Semantic Analysis, 잠재 의미 분석)

지난 [DL] 자연어 처리에서의 텍스트 표현 - 단어 임베딩(Word Embedding) 포스트에서 SVD와 이를 사용한 LSA에 대해 알아봤었다. 다시 한 번 정리하자면, LSA는 co-occurrence matrix를 만든 후 행렬을 수치화해서 단어 벡터를 만들어내는 방식 중 하나이다. 이때 co-occurrence matrix란 단어가 동시에 등장하는 횟수를 하나의 행렬로 나타낸 것으로, 의미가 가까운 단어-문서, 단어-단어, 문서-문서를 찾을 수 있게 해준다.

또 하나의 핵심 개념은 차원 축소(dimensionality reduction)이다. 가령 아래와 같은 원본 행렬 $ A$가 있다고 해보자.

full SVD를 이용해 3개의 행렬로 나눈다면 다음과 같은 형태가 될 것이다.

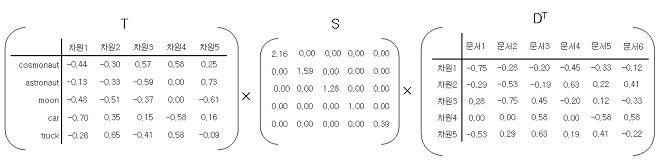
지금은 5차원~6차원 선에서 해결이 되지만 실제 문서 하나를 두고 co-occurrence matix를 만든다면 수만 차원이 될 것이다. 여기서 truncated SVD를 사용해 임의의 값 $ k$를 설정하고, $ k$ 이상의 차원은 없애버리는 방법으로 차원을 축소할 수 있다.

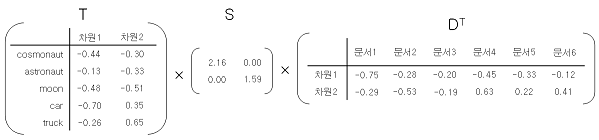
이렇게 형성된 3개의 행렬에 대해 $TSD^T$의 각 요소에 대한 코사인 유사도를 계산하면 된다. 어떤 행렬을 조합하는지에 따라 시나리오가 다르기 때문에 아래를 참고.

1. 단어 - 단어간의 유사도 $T X S $ 행렬의 row 간의 유사도로 계산한다.
2. 문서 - 문서 $S X D^T$ 행렬의 colum 간의 유사도로 계산한다.
3. 단어 - 문서 $TSD^T $의 각 요소가 단어와 문서간의 유사도이다.

- 출처 : https://sragent.tistory.com/entry/Latent-Semantic-AnalysisLSA

2. LDA (Latent Dirichlet Allocation, 잠재 디리클레 할당)

참고 영상 - https://www.youtube.com/watch?v=1_jq_gWFUuQ

직관적으로 생각하면 LDA 모델은 함께 자주 나타나는 단어의 그룹을 찾는 것이다. LDA는 각 문서에 토픽의 일부가 혼합되어 있으며, 토픽들은 확률 분포에 기반하여 단어들을 생성한다고 간주한다.

문서군을 $ D$라고 표기하고 각각의 문서를 $d$라고 해보자. 마찬가지로 토픽군을 $K$라 하고 각각의 토픽을 $k $라고 해보자. 위의 그림에서는 $ d=1, 2, 3$의 문서가 있으며 토픽 $ k=1, 2, 3, 4$가 존재한다. 위에서 말했듯이 LDA는 확률 분포에 기반한다. 가령 사람이라면 $d=1$ 문서를 토픽 $k=2, 3$에 해당한다고 말하겠지만, LDA는 $d=1$ 문서에 토픽의 확률분포에 대한 벡터 $ \Theta_1 = [0, 0.5, 0.5, 0] $를 할당할 것이다.

각각의 문서에 확률분포 기반의 벡터 $ \Theta_d $를 할당한 모습

각각의 $ \Theta_d $는 디리클레 분포에서 도출된, 우리가 알고자 하는 임의의 변수와 같다고 말할 수 있다.

디리클레 분포

간단히 말하자면 디리클레 분포란 $k$차원의 실수 벡터 중 벡터의 요소가 양수이며, 모든 요소를 더한 값이 1인 경우에 확률값이 정의되는 연속확률분포이다. 2 이상의 자연수 $k$와 양의 상수 $ \alpha_1, ..., \alpha_k $에 대하여 디리클레 분포의 확률밀도함수는 다음과 같이 정의된다.

$ x_1, ..., x_k$가 모두 양의 실수이며 $ \sum_{i=1}^k x_i = 1 $을 만족할 때,

$$ f(x_1, ..., x_k; \alpha_1, ..., \alpha_k) = \frac{1}{B(\alpha)} \prod_{i=1}^k x_i^{\alpha_i-1} $$

$$ B(\alpha) = \frac{\prod_{i=1}^k\gamma(\alpha_i)}{\gamma(\sum_{i=1}^k\alpha_i)} $$

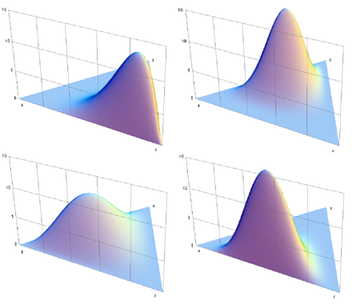
다양한 값에 대한 3차원 디리클레 분포의 모습. 왼쪽 위에서부터 시계방향으로 =(6, 2, 2), (3, 7, 5), (6, 2, 6), (2, 3, 4)이다.

이해가 어렵다면 그냥 이 분포에서 도출된 임의의 변수 벡터의 원소 합이 1이 되어야 한다는 것을 기억하면 된다... 즉 각 $ \Theta_d $에 대해 확률질량함수로 동작하는 것.

LDA 접근방식은 각 문서의 각 단어 특정 주제에 속한다고 가정하는 것에서 출발한다. 즉, 각각의 주제 $k$는 단어의 전체 어휘에 대한 고유한 분포를 가지고 있다는 것이다. 예시로 돌아가, 첫번 째 토픽 science에 속하는 단어들에 대해 생각해보자. argon, ball, cry,... 라는 단어가 이어진다면, 토픽 science에 대한 단어의 확률 분포 $ \beta_1 = [0.01, 0, 0, ...] $ 이렇게 생겼을 것이다(토픽 science 하에서 단어 argon이 생성될 확률이 ball이나 cry보다는 좀 더 높기 때문에)

$ \beta_1$에 이어 다른 각각의 토픽에 대한 단어의 확률 분포를 완성한 모습

해당 확률 분포도 모두 어떠한 디리클레 분포에서 기인했음을 알 수 있다.

이제 LDA 접근방식을 사용해 문제를 해결할 수 있도록 하는 변수들이 모두 정의되었다. 여기까지는 LDA가 가정하는 문서 생성과정을 살펴보았으니, 이제 역으로 잠재변수를 추정하는 inference 과정을 살펴볼 것이다. LDA는 토픽의 단어분포와 문서의 토픽 분포를 가지고 문서 내 단어들이 생성된다고 가정한다. Inference 과정은 관찰가능한 문서 내 단어를 가지고 우리가 알고 싶은 토픽의 단어분포, 문서의 토픽분포를 추정하는 반대의 과정이다.

LDA가 가정하는 문서 생성과정이 합리적이라면 토픽의 단어분포와 문서의 토픽분포의 결합확률이 커지도록 해야 한다. 즉, 관찰한 문서군 안에서 최적의 $ \Theta_d$ 및 $ \beta_d $ 확률 분포 벡터를 학습하는 것이다.

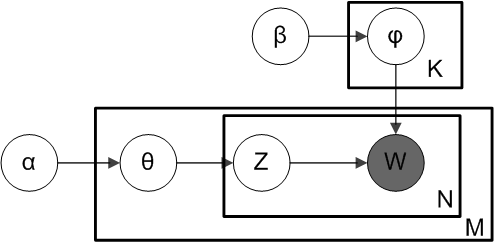
$ w_{nd}$를 문서 $d$의 $n$ 번째 단어라고 할 때,

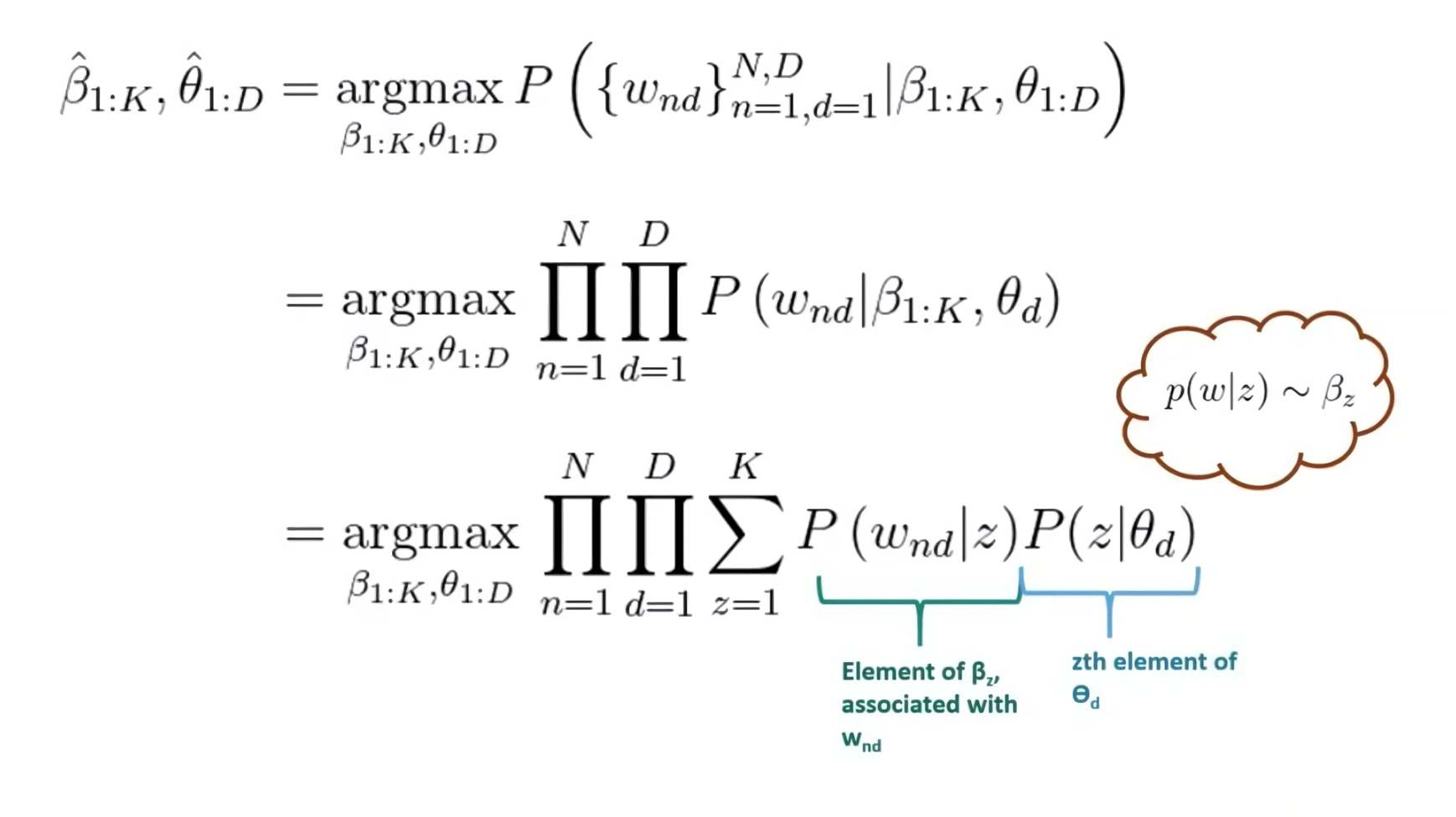
$ z$: 단어에 할당된 토픽 인덱스를 나타내는 잠재 변수(어떠한 단어가 속한 토픽의 번호)
토픽 $z$에 대한 모든 단어의 분포인 $ \beta_z $를 사용하여 어떤 단어 $w$의 확률을 정확하게 찾을 수 있음

Gibbs sampling (깁스 샘플링)

깁스 샘플링 개념은 위의 computation에서 단어가 늘어나면 늘어날수록 계산량이 기하급수적으로 나타나기 때문에 적용되었다. 깁스 샘플링은 $N$개의 자료 중 $N-1$개를 고정하고 한 차원에 대한 자료만 샘플링한 후 합치는 방식으로 진행된다.

$$ p(z_i=j|z_{-i}, w) $$

이러한 계산 과정을 거치고 나면 최종적으로 $ $d$ 번째 문서 \( $i$ 번째 단어의 토픽 \( z_{d,i} $가 $ j $번째에 할당될 확률은 다음과 같다. ~~아 힘들어....~~

$$ p(z_{d, i}=j|z_{-i}, w) = \frac{n_{d, k}+\alpha_j}{\sum_{i=1}^K (n{d, i}+\alpha_i)} \times \frac{v_{k, w_{d,n}}+\beta_{w_{d,n}}}{\sum_{j=1}^V(v_{k,j}+\beta_j)} = AB $$

$ n_{d, k} $ = $k $번째 토픽에 할당된 $d$ 번째 문서의 단어 빈도
$ v_{k, w_{d,n}} $ = 전체 어휘에서 $ k$ 번째 토픽에 할당된 단어 $ w_{d,n} $의 빈도
$ V $ = 등장하는 전체 단어 수
$ A $ = $ d$ 번째 문서가 $ k$ 번째 토픽과 맺고 있는 연관성의 정도
$ B $ = $ d$ 번째 문서의 $ n$ 번째 단어 $ w_{d,n}$가 $ k$ 번째 토픽과 맺고 있는 연관성의 정도

LSA vs LDA

LSA : DTM을 truncated SVD를 통해 축소하여 축소 차원에서 근접 단어들을 토픽으로 묶는다.
LDA : 단어가 특정 토픽에 존재할 확률과 문서에 특정 토픽이 존재할 확률을 결합확률로 추정하여 토픽을 추출한다.

자료 출처 : https://wikidocs.net/30708

https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/06/01/LDA/