[ML] GBM 알고리즘 및 LightGBM 소개글에서 부스팅 앙상블 학습과 GBM이란 무엇인지 소개한 적이 있다. 사실 GBM 설명 이후에 LightGBM이 바로 나오는게 아니라 XGBoost가 먼저 나왔어야 했다... 왜냐하면 LightGBM이나 CatBoost는 다 XGBoost를 보다 강력하게 만드려는 시도에서 나온 것이기 때문이다. 따라서 오늘은 XGBoost를 살펴보려고 한다.
XGBoost: A Scalable Tree Boosting System 논문 참고!
1. XGBoost 알고리즘 특징 소개
논문은 다음과 같은 contribution들을 나열한다.
- We design and build a highly scalable end-to-end tree boosting system.
- We propose a theoretically justified weighted quantile sketch for efficient proposal calculation.
- We introduce a novel sparsity-aware algorithm for parallel tree learning.
- We propose an effective cache-aware block structure for out-of-core tree learning.
첫 번째 줄은 그냥 전체 시스템의 대략적인 소개같은 거라서 패스 필자도 XGBoost의 강점으로 결손값을 자체 처리하는 기능이 있다고 들었다. 그리고 예측 성능이 좋고 GBM 대비 수행 시간이 빠르다는 점도.. 밑에서 차차 설명해보도록 하겠다.
Weighted Quantile Sketch
트리 부스팅 앙상블 모델에서 최소화해야되는 목적함수(손실함수)는 다음과 같이 정의된다(approximated version).
$$ \widetilde{L}^{(t)}(q) = -\frac{1}{2}\sum_{j=1}^T\frac{(\sum_{i\in I_j} g_i)^2}{\sum_{i\in I_j} h_i+\lambda} + \gamma T $$
- q는 각 트리의 구조(독립적), T는 해당 트리에 있는 리프(노드)의 개수, \( g_i \)와 \( h_i \)는 목적함수에 대한 1계 및 2계 gradient 통계량, t는 스텝
- i 번째 리프를 상정하고 계산한다.
- \( I_j = \begin{Bmatrix} i|q(x_i)=j \end{Bmatrix} \)을 리프 j의 인스턴스 집합으로 정의
이 공식은 트리 q의 quality를 측정하는 scoring function으로 사용할 수 있는데, 해당 점수는 더 넓은 범위의 목적함수에 대해 도출된다는 점을 제외하고는 결정트리를 평가하기 위한 불순도 점수(impurity score)와 같다.
통상적으로, 가능한 모든 트리 구조 q를 열거하는 것은 불가능하기 때문에 단일 리프로부터 시작해 트리에 반복적으로 가지를 추가하는 greedy algorithm이 대신 사용된다. \( I_L \)과 \( I_R \)을 분할 후 왼쪽과 오른쪽 리프의 인스턴스 집합이라고 가정하면, 식
$$ L_{split} = \frac{1}{2} \begin{bmatrix} \frac{(\sum_{i\in I_L} g_i)^2}{\sum_{i\in I_L} h_1+\lambda} + \frac{(\sum_{i\in I_R} g_i)^2}{\sum_{i\in I_R} h_1+\lambda} - \frac{(\sum_{i\in I} g_i)^2}{\sum_{i\in I} h_1+\lambda} \end{bmatrix} - \gamma $$
이 loss reduction이 되며 분할 후보(split candidate)를 측정하는 데에 사용된다.
트리 학습의 핵심 문제 중 하나는 위의 공식으로 도출되는 최상의 분할 지점을 찾는 것이다. 이를 위해 split finding algorithm은 모든 피처에 대해 가능한 분할을 열거한다. 우리는 이것을 exact greedy algorithm이라고 부른다. scikit-learn, R의 gbm, 단일 머신 버전의 XGBoost 등 대부분의 기존 단일 머신 트리 부스팅 구현은 exact greedy algorith을 지원한다. Exact greedy algorithm은 가능한 모든 분할 지점에 대해 greedy하게 enumerate하기 때문에 매우 강력하지만, 데이터가 전부 메모리에 올라갈 수 있을 정도의 양이 아닐 경우 효율적으로 수행되기 불가능하다. 따라서 효과적인 그래디언트 부스팅을 지원하려면 approximated 알고리즘이 필요하다. 이때 등장하는 것이 weighted quantile sketch인데, 요약하자면 먼저 피처 분포의 백분위수(quantile)에 따라 후보 분할 지점을 제안한다. 그런 다음 continuous 피처들을 이러한 후보 지점에 의해 분할된 버킷(bucket)으로 매핑하고 통계를 aggregate한다. 이렇게 aggregated된 통계값들을 기반으로 proposal들 중 최상의 솔루션을 찾는 것이다.
multi-set \( D_k = \begin{Bmatrix} (x_{1k}, h_1), (x_{2k}, h_2), ..., (x_{nk}, h_n) \end{Bmatrix} \)가 있고 \( h_i \)를 데이터 포인트의 가중치라고 할 때, 목표는
$$ |r_k(s_{k,j}) - r_k(s_{k,j+1})| < \varepsilon , s_{k1}=min x_{ik}, s_{kl} = max x_{ik} $$
- \( \varepsilon \)은 approximation factor
- 직관적으로 \( 1/\varepsilon \)만큼의 candidate point가 있음을 뜻한
와 같은 후보 분할점 \( \begin{Bmatrix} s_{k1}, s_{k2}, ..., s_{kl} \end{Bmatrix} \)을 찾는 것이다.
데이터가 많은 대규모 데이터셋에서는 이 기준을 충족하는 후보 분할을 찾는 것은 non-trivial(자명해서 사소함)하다. 모든 인스턴스의 가중치가 동일할 경우, 'quantile sketch'라는 이미 존재하는 알고리즘으로 문제를 해결할 수 있다. 그러나 가중치가 있는 데이터셋에 대해서는 기존의 정량적 스케치는 없다. 따라서 입증 가능한 이론적 보증으로 가중 데이터를 처리할 수 있는 새로운 distributed weighted quatile sketch 알고리즘을 도입한 것이다! 일반적인 아이디어는 병합(merge) 및 제거 연산(prune)을 지원하는 데이터 구조를 사용하고, 각 연산은 특정 정확도 수준을 유지하는 것으로 입증된다.
Sparsity-aware Split Finding
Sparsity(희소성)은 차원/전체 공간에 비해 데이터가 있는 공간이 매우 협소한 데이터를 의미한다.

위의 사진에서 행렬의 값 대부분이 0이다. 0이란 값이 할당되어 있지 않다는 것이기 때문에, 이 행렬의 데이터 대부분이 유효하지 않다는 뜻이 된다. 머신러닝에서는 이런 희소한 데이터를 가지고 학습을 할 시 학습이 잘 되지 않는다.
데이터의 희소성에는 여러 가지 원인이 있을 수 있다.
- 데이터에 결측값이 존재
- 통계값에서의 빈번한 0
- 원-핫 인코딩과 같은 feature engineering artifact
이런 희소성에 의한 디메리트를 줄이려면, 알고리즘이 데이터의 희소성 패턴을 인식하도록 하는 것이 중요하다. XGBoost는 이를 위해 각 트리 노드에 'default direction'을 추가한다.
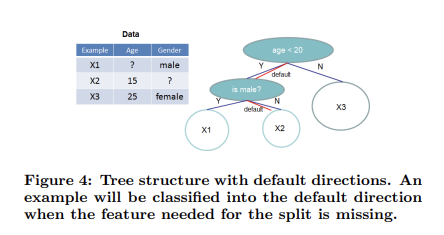
희소행렬 x에 value가 없으면, 인스턴스는 default direction으로 분류된다. 각 분기에는 두 가지의 default direction 선택지가 있는데, 최적의 default direction은 데이터로부터 학습된다.

핵심적인 개선 방향은 결측되지 않은 entry \( I_k \)만 방문함으로써, 존재하지 않는 값을 결측치로 처리하고 결측치를 다루는 가장 좋은 direction을 학습한다는 것이다. 이는 존재하는 다른 트리 학습 알고리즘이 밀집 데이터(dense data)를 처리하는 데에만 최적화되어 있거나, 범주형 인코딩과 같이 한계를 다루는 특별한 단계가 필요한 것에 비해 통합된 방법으로 희소 패턴을 처리한다는 점에서 뛰어나다.
Cache-aware block structure
Column Block for Parallel Learning
트리 학습에서 가장 많은 시간이 소요되는 부분은 데이터를 정렬하는 것이다. XGBoost는 정렬 비용을 줄이기 위해 데이터를 메모리 내(in-memory) unit에 저장할 것을 제안한다(In-memory가 무엇인지 모르는 나와 여러분들을 위해... https://www.hpe.com/kr/ko/what-is/in-memory-computing.html 이곳을 참고하세요). 이를 block이라고 한다. 각 block의 데이터는 compressed column(CSC) 형식으로 저장되는데, 각 column을 해당 feature 값 별로 정렬한 것이다. 이 입력 데이터 layout은 학습 전에 한 번만 계산하면 되고 이후 iteration에서 다시 사용할 수 있다.
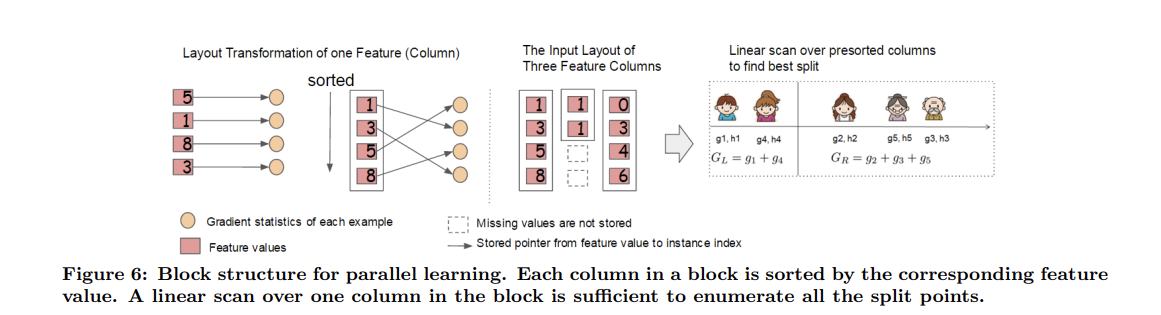
Exact greedy algorithm에서는 전체 데이터셋을 단일 블록에 저장하고, 사전 정렬된 엔트리에 대해 선형 스캐닝(linear scanning)하여 분할 검색 알고리즘을 실행한다. 모든 노드의 분할지점을 집합적으로 찾아내기 때문에, block을 한 번 스캔하면 모든 노드 가지에서 분할된 후보들의 통계를 수집할 수 있다. 이러한 block 구조는 approximate algorithm을 사용할 때도 도움을 준다. 서로 다른 block들은 여러 기계들에 분산되거나 out-of-core 환경의 디스크에 저장될 수 있다. 즉, column에 대한 통계량을 수집하는 이러한 과정은 병렬적으로 이루어질 수 있으며(parallelized), 이는 분할 탐지에 대한 병렬 알고리즘을 제공한다. (그래서 parallel tree learning이라고 부르나보다)
Cache-aware Access
위에서 제안된 block 구조가 split finding의 계산 복잡도를 최적화하는 데에 도움이 되는데, 이 새로운 알고리즘은 행 인덱스를 기준으로 gradient 통계량을 간접적으로 가져온다. 이 값들은 피처의 순서대로 접근되기 때문이다. 이것은 비연속 메모리 접근(non-continuous memory access)이다. Split enumeration의 단순한 구현은 축적과 비연속적인 메모리 접근 사이에 즉각적인 read/write 의존성을 도입한다.
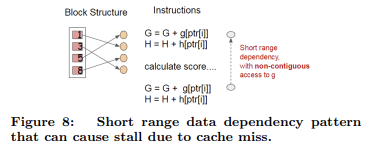
Exact greedy algorithm의 경우 cache-aware prefetching algorithm을 통해 위의 문제를 완화할 수 있다. 특히, XGBoost는 각 스레드에 내부 버퍼를 할당하고, gradient 통계량을 가져온 다음 미니 배치(mini batch) 방식으로 축적을 수행한다. 이 prefetch는 direct read/write 종속성을 더 긴 종속성으로 변경하고, 행의 수가 많을 때 런타임 오버헤드를 줄이는 데에 도움이 된다.
Approximate algorithm의 경우 올바른 block size를 선택하여 문제를 해결한다. block size는 gradient 통계량의 캐시 스토리지 비용을 반영하기 때문에 block에 포함된 개체의 최대 수로 정의한다. 지나치게 작은 block size를 선택하면 각 스레드의 워크로드가 작아지고 비효율적인 병렬화가 초래된다. 반면, 지나치게 큰 block은 CPU 캐시에 gradient 통계량이 맞지 않기 때문에 캐시 누락을 발생시킨다. block size를 잘 선택하면 이 두 요소가 균형을 이루게 된다. 논문에 의하면 block 당 \( 2^{16} \)개의 개체를 선택하면 cache property와 병렬화가 균형을 이룬다고 한다.
'AI > Machine Learning' 카테고리의 다른 글
| [ML] 토픽 모델링(Topic Modeling) - LSA와 LDA (0) | 2022.03.13 |
|---|---|
| [ML] 앙상블(Ensemble Learning) - Voting, Bagging, Boosting (0) | 2021.10.18 |
| [ML] CatBoost 소개 - Ordered Boosting, 범주형 피처 처리 (0) | 2021.10.08 |
| [ML] GBM 알고리즘 및 LightGBM 소개 - 기본구조, parameters (0) | 2021.10.08 |
| [ML] 결정트리(Decision Tree) - 기본구조와 CART, ID3 알고리즘 (1) | 2021.10.03 |



