평가지표의 중요성
통상적으로 정확도(accuracy)를 사용해 머신러닝이나 딥러닝 모델을 평가하곤 한다. 하지만 주어진 데이터셋에 대한 모델의 성능을 재는 방법은 그 외에도 많다. 실전에서 어떻게 적용할지에 따라 특정 평가 지표가 적합하지 않을 수 있으므로, 모델을 선택하고 하이퍼 파라미터를 튜닝할 때 올바른 지표를 선택하는 것이 중요하다.
불균형 데이터셋(imbalanced datasets)을 기반으로 이진 분류기를 만든다고 가정해보자. 대표적으로 어떤 아이템이 사용자에게 보여진 노출 데이터로 클릭을 예측하는 상황을 들 수 있다. 최종 목표는 특정 상품을 보여주면 사용자가 클릭을 할지 예측하는 것이다. 데이터셋은 '특정상품을 보여줌->클릭하지 않음(0)'과 '특정상품을 보여줌->클릭함(1)'로 나누어져 있고, 이를 기반으로 지도 학습 모델을 만들어야 한다. 경영자들에게는 안타깝지만, 인터넷에서 볼 수 있는 정보 대부분은 (특히 광고는) 클릭까지 이어지지 않는다. 그래서 사용자가 관심을 보일 때까지 상품을 100개나 보여줘야 할 수도 있다. 아무튼 다르게 말하면 샘플의 99%가 '클릭하지 않음(0)' 클래스에 속하게 된다. 이처럼 한 클래스에 속하는 샘플의 수가 다른 것보다 훨씬 많은 데이터셋을 불균형 데이터셋이라 한다. 이제 클릭을 99%의 정확도로 예측하는 분류기를 만들었다고 해보자. 정확도 99%면 엄청 좋은 모델 같아보인다. 실제로는 이게 무슨 뜻일까? 이미 데이터셋의 99%는 0의 클래스에 속하기 때문에 굳이 머신러닝 모델을 만들지 않더라도 모두 '클릭하지 않음'으로 예측하면 정확도가 99%이다. 즉, '정확도 99%'는 아주 좋은 수치가 맞지만, 실제로 사용하게 되면 별로 좋은 모델이 아닐 가능성이 높다(1 클래스를 제대로 예측하지 못할 것이다. 근데 이 경우에는 사람들이 클릭하는 패턴을 학습해 노출도를 올리는 것이 목표이기 때문에 1을 예측하는 것이 어마어마하게 중요하다). 이처럼 불균형 클래스를 고려하지 않고 정확도로만 모델을 평가하면 '진짜 좋은 모델'이 무엇인지 판단하기 힘들다. 따라서 데이터셋의 특징이나 최종 목표를 따져보면서 어떤 방법으로 모델의 성능을 측정해야할지 고민하는 시간이 필요하다.
이번 포스트에서는 모델의 성능을 측정하는 여러 가지 방법들에 대해 소개해보겠다.
1. 오차행렬 (confusion matrix)
오차행렬은 이진 분류 평가 결과를 나타낼 때 가장 많이 쓰이는 방법 중 하나로, 총 4가지 항목으로 구성된다.
mglearn.plots.plot_binary_confusion_matrix()
- TP (True Positive) - 양성을 양성이라고 예측
- TN (True Negative) - 음성을 음성이라고 예측
- FP (False Positive) - 음성을 양성이라고 예측: Type 1 error
- FN (False Negative) - 양성을 음성이라고 예측: Type 2 error
양성과 음성으로 암환자를 판단한다고 해보자. 테스트가 음성이면 건강하다는 뜻이고, 양성이면 추가 검사를 받아야 한다. 건강한 사람을 건강하다고 판단한다거나(TN) 양성인 사람을 양성으로 판단하는 것(TP)은 문제가 되지 않는다. 하지만 건강한 사람을 양성으로 판단해버리면(FP), 환자가 쓸데없는 비용을 지불하고 시간을 낭비하게 된다. 이를 거짓 양성이라고 한다. 반대로 양성인 사람을 음성으로 판단해버리면(FN)? 이 사람은 암을 발견하지 못하고 살다가 죽어버릴 수도 있다. 이를 거짓 음성이라고 하며, 암 진단의 예에서는 거짓 음성을 최대한 피하는 것이 최우선 중요도를 가진다.
정확도 (accuracy)
정확도는 오차행렬의 결과를 요약함으로써 얻어질 수 있다.
$$ accuracy = \frac{TP + TN}{TP + TN + FP + FN} $$
즉, 정확도는 [정확히 예측한 수(TP와 TN) / 전체 샘플 수(오차행렬의 모든 항)]이다.
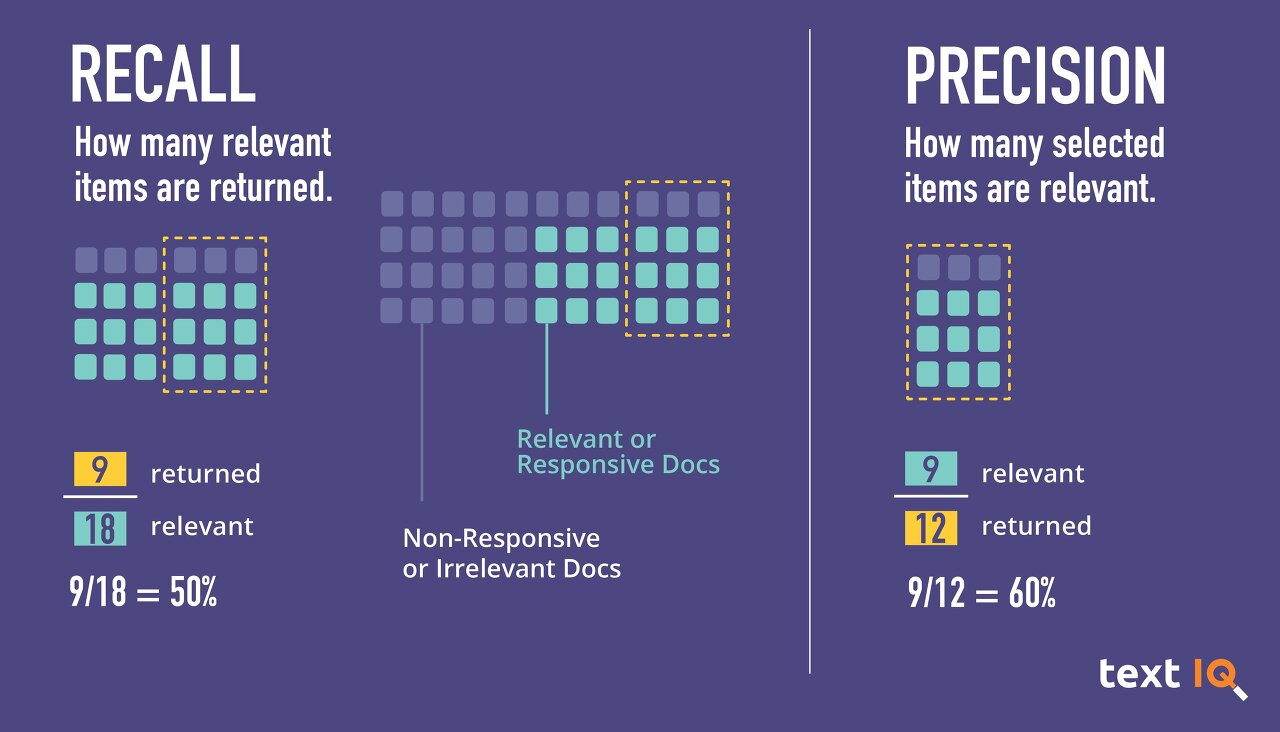
정밀도 (precision)
정밀도는 양성으로 예측된 것(TP+FP) 중 얼마나 많은 샘플이 진짜 양성(TP)인지 측정한다. 다른 말로는 양성 예측도(PPV)라고도 한다.
$$ precision = \frac{TP}{TP + FP} $$
재현율 (recall)
재현율은 전체 양성 샘플(TP+FN) 중에서 얼마나 많은 샘플이 진짜 양성(TP)인지 측정한다. 다른 말로는 민감도(sensitivity), 적중률(hit rate), 진짜 양성 비율(TPR)이라고도 한다.
$$ recall = \frac{TP}{TP + FN} $$
F1-점수 (F1-score)
f1-점수는 정밀도와 재현율의 조화 평균이다. 정밀도와 재현율을 같이 고려하므로 불균형한 이진 분류 데이터셋에서는 정확도보다 더 나은 지표가 될 수 있다.
$$ F = 2 \times \frac{precision \cdot recall}{precision+recall} $$
precision VS recall ?
정밀도 최적화와 재현율 최적화는 동시에 이루어질 수 없다. 정밀도와 재현율의 식을 보면, 분모에 FP가 있는지 아니면 FN이 있는지만 다르다. 음성을 양성이라고 판단하는 거짓 양성(FP)을 최소화하는 일과, 양성을 음성이라고 판단하는 거짓 음성(FN)을 최소화하는 일은 상충한다. 예컨대 모든 샘플을 진짜 음성(TN)이 하나도 없고 모두 양성 클래스에 속한다고 예측하면, FN은 0이 된다(애초에 음성으로 분류하지를 않아버리는 것이다). 반면, 이렇게 되면 실제로 음성인 데이터를 모두 양성이라고 예측하기 때문에 FP를 많이 만들게 된다. 반대의 상황도 똑같다. 따라서 정밀도와 재현율은 매우 중요한 측정 방법이지만, 둘 중 하나만으로는 전체 그림을 볼 수 없기 때문에 둘을 적절히 섞는 F1-점수를 이용하는 것이다.
2. 정밀도-재현율 곡선 (precision-recall curve; PRC)
그렇다면 정밀도와 재현율 둘 다의 최적화는 불가능한 것인가? 모델을 어디에 어떻게 쓸 것인지가 중요하다. 예를 들면 어떤 공장에서는 불량품 샘플을 멀쩡하다고 잘못 분류하는 실수(FN)를 10%보다 작게 하여 90% 이상의 재현율을 원할 수 있다. 이렇게 모델의 분류 작업을 결정하는 임계값(threshold)을 바꾸는 것은 해당 분류기의 정밀도와 재현율의 상충 관계를 조정하는 일이다. '90%의 재현율'처럼 분류기의 필요조건을 지정하는 것을 운영 포인트(operating point)를 지정한다고 말한다. 새로운 모델을 만들 때는 운영 포인트가 명확하지 않은 경우가 많은데, 이런 경우에는 모든 임계값을 조사해보거나 한 번에 정밀도와 재현율의 장단점을 살펴보는 것이 좋다. 이를 위해 정밀도-재현율 곡선(PRC)을 사용한다.
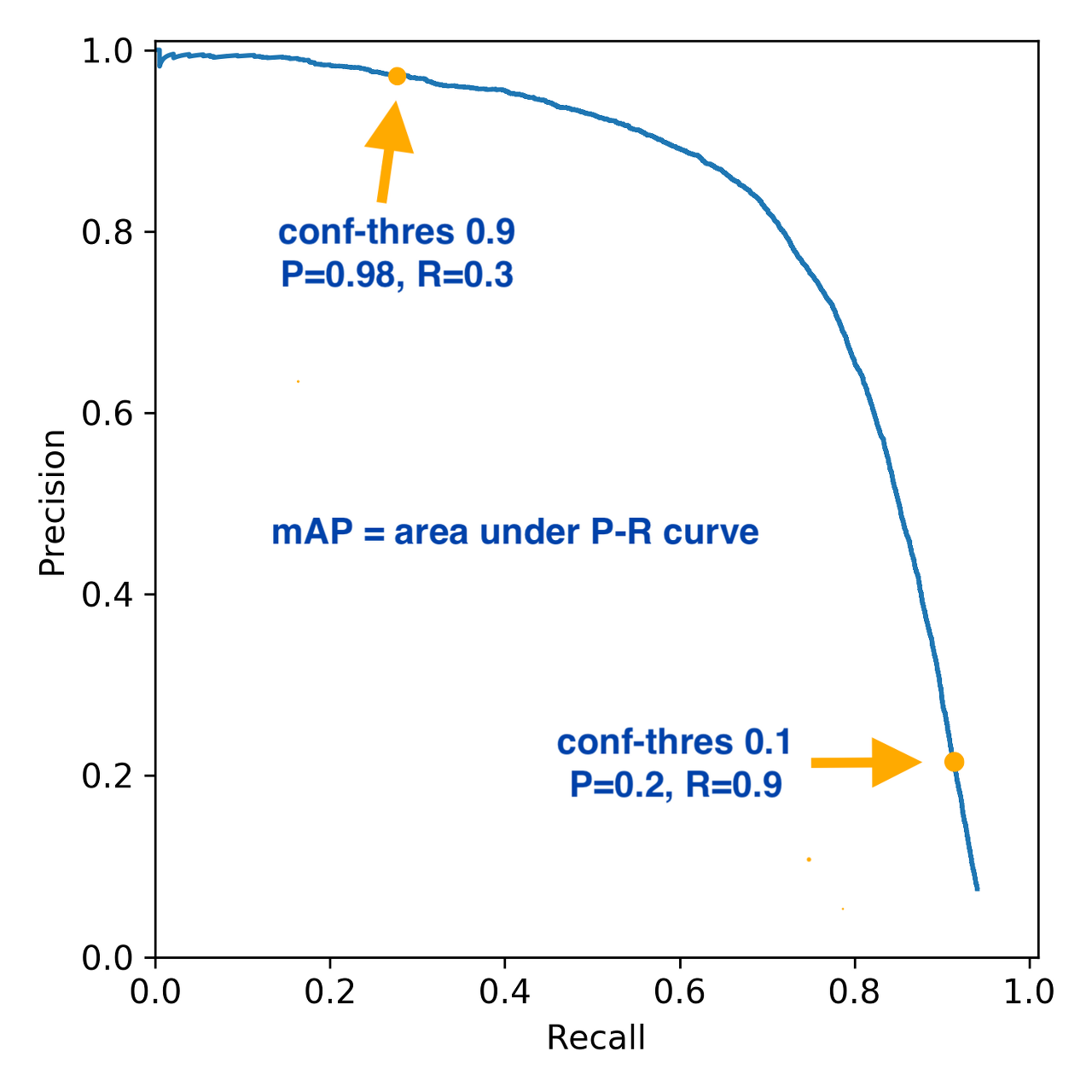
PRC이 오른쪽 위로 솟아있을수록 더 좋은 분류기이다. 오른쪽 위 지점은 한 임계값에서 정밀도와 재현율이 모두 높은 곳이기 때문이다.
AUPRC (Area under the Precision-Recall Curve)
여러 개의 분류기 중 하나를 고르기 위해 모든 분류기의 PRC를 비교하는 것은 수작업을 필요로 한다. 모델을 자동으로 비교하려면, 특정 임계값이나 운영 포인트에 국한하지 않고 전체 곡선에 담긴 정보를 요약해야 한다. AUPRC는 PRC 아래의 면적 값으로, 정밀도와 재현율 모두 1에 가까울수록 좋기 때문에 AUPRC의 값도 1에 가까울수록 좋은 모델이다.

평균 정밀도 (average precision)
AUPRC와 평균 정밀도 사이에는 미묘한 기술적 차이가 있으나 일반적으로는 PRC 아랫부분의 면적이라고 이해된다(아무도 두 값의 차이에 대해 알려주지 않는다... 그래서 scikit-learn의 average_precision_score 공식 도큐먼트에서 설명을 따왔다)
AP summarizes a precision-recall curve as the weighted mean of precisions achieved at each threshold, with the increase in recall from the previous threshold used as the weight:
$$ AP = \sum_n (R_n - R_{n-1})P_n $$
where \( P_n \) and \( R_n \) are the precision and recall at the nth threshold. This implementation is not interpolated and is different from computing the area under the precision-recall curve with the trapezoidal rule, which uses linear interpolation and can be too optimistic.
"This implementation is not interpolated and is different from computing the area under the precision-recall curve with the trapezoidal rule, which uses linear interpolation and can be too optimistic." 이라는 설명을 보니 AUPRC는 선형 보간법을 사용해 어느정도 값을 근사시켜 면적을 구하는 것 같고, 평균 정밀도는 그렇지 않은 것 같다.
3. ROC와 AUC
ROC 곡선은 진짜 양성 비율(TPR)에 대한 거짓 양성 비율(FPR)을 나타낸다. TPR은 재현율의 또 다른 이름이며, FPR은 전체 음성 샘플 중에서 거짓 양성으로 잘못 분류한 비율이다.
$$ FPR = \frac{FP}{FP + TN} $$
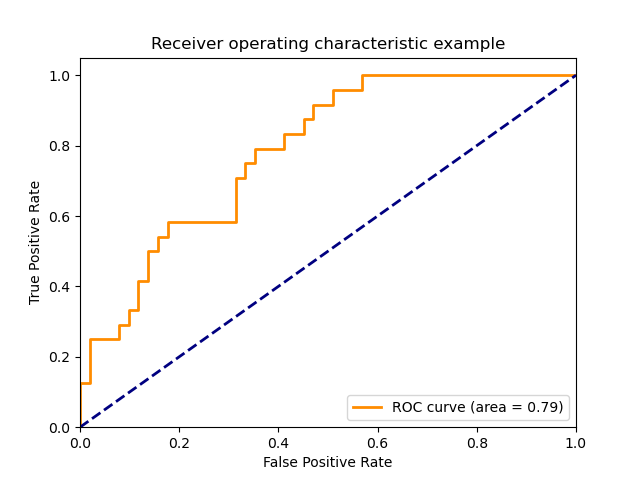
ROC 곡선은 왼쪽 위에 가까울수록 이상적이다. FPR이 낮게 유지되면서 재현율이 높은 분류기가 좋은 것이다.
PRC에서처럼 곡선 아래의 면적값 하나로 ROC 곡선을 요약할 수 있다. 이 면적을 보통 AUC라고 하므로, ROC 곡선 아래의 면적값은 AUROC라고 부르기도 한다. AUC가 0과 1 사이의 곡선 아래의 면적이므로 항상 0(최악)과 1(최선) 사이의 값을 가진다. FPR과 TPR은 오차행렬에서 각각 다른 행을 이용하여 만들기 때문에 클래스의 불균형이 FPR과 TPR 계산에 영향을 주지 않는다. 무작위로 분류하면 클래스별 양성과 음성 비율이 비슷해서 FPR과 TPR 값이 거의 같아지므로, ROC 곡선은 \( y=x \)에 가깝게 되어 AUC 면적은 0.5가 된다. 그래서 불균형한 데이터셋에서는 정확도보다 AUC가 훨씬 좋은 지표이다.
다중 클래스에서의 평가
위에서 본 ROC, AUC 등은 이진 분류 평가 방식이다. 실제로 공식 도큐먼트 들어가보면 "Note: this implementation is restricted to the binary classification task or multilabel classification task."라고 쓰여있음. 다중 분류를 위한 지표는 모두 이진 분류 평가 지표에서 유도되었으며, 다만 모든 클래스에 대해 평균을 낸 것이다. 다중 분류의 정확도도 정확히 분류된 샘플의 비율로 정의한다. 그래서 클래스가 불균형할 때는 정확도가 좋은 평가 방법이 되지 못한다. 그래서 f1-점수의 다중 분류 버전을 가장 널리 이용한다. scikit-learn에서의 f1-score 함수를 이용한다면 average 파라미터를 사용하면 된다.
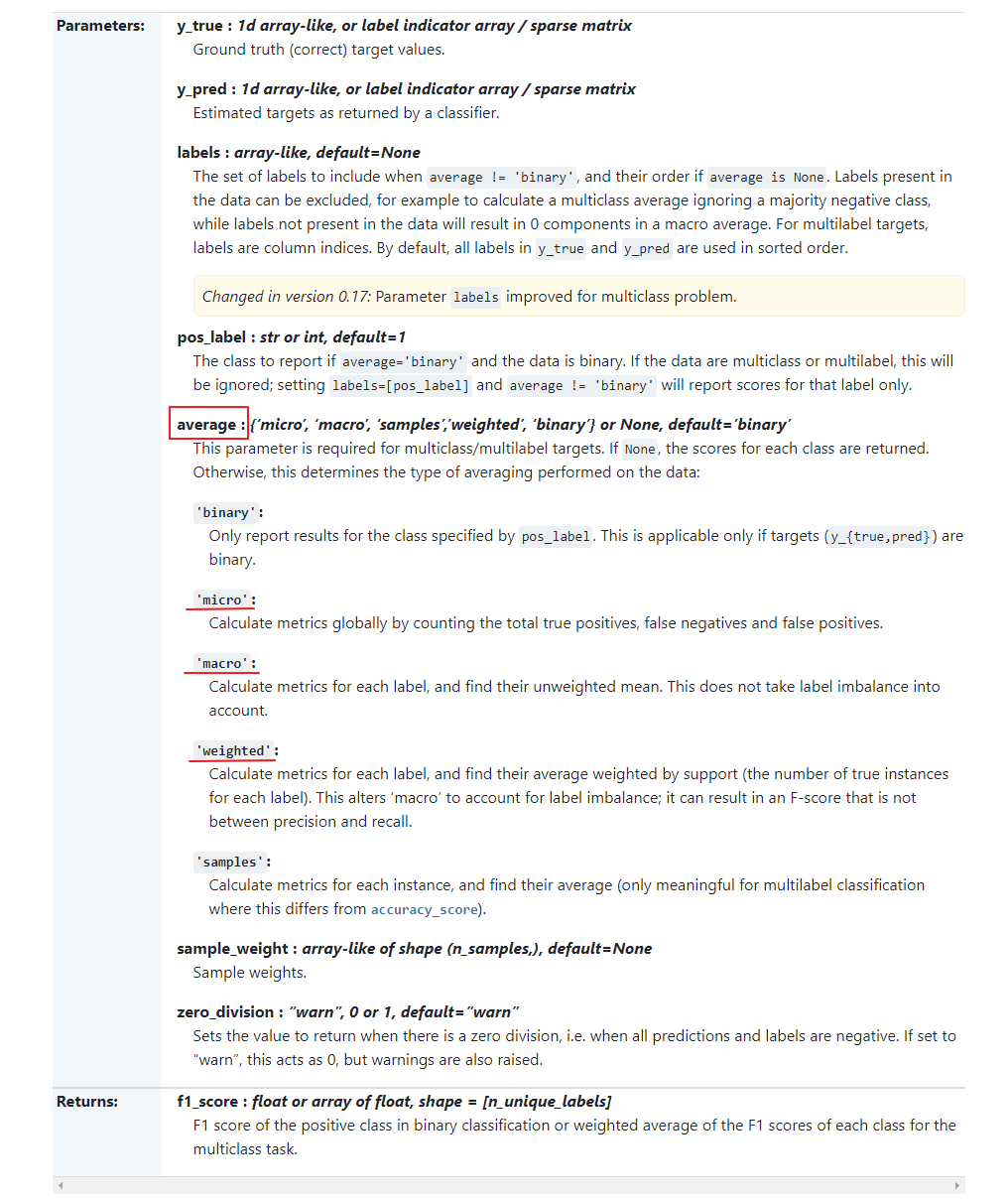
- macro : 클래스 크기에 상관없이 모든 클래스를 같은 비중으로 f1-score 계산 (가중치X)
- micro : 모든 클래스의 FP, FN, TP의 총 수를 헤아린 다음 정밀도, 재현율, f1-score를 이 수치로 계산
- weighted : 클래스별 샘플 수로 가중치를 두어 f1-score의 평균을 계산
'AI > Machine Learning' 카테고리의 다른 글
| [ML] GBM 알고리즘 및 LightGBM 소개 - 기본구조, parameters (0) | 2021.10.08 |
|---|---|
| [ML] 결정트리(Decision Tree) - 기본구조와 CART, ID3 알고리즘 (1) | 2021.10.03 |
| [ML] 범주형 변수 처리 - Label Encoding, One-hot Encoding (0) | 2021.09.29 |
| [ML] 활성화 함수(Activation Function) 종류 정리 (0) | 2021.09.29 |
| [ML] 신경망에서의 Optimizer - 역할과 종류 (0) | 2021.09.28 |



